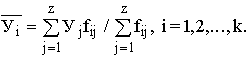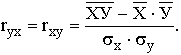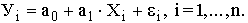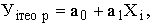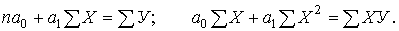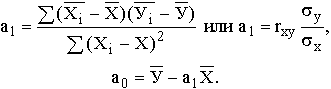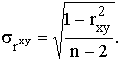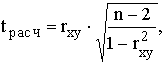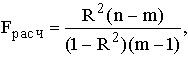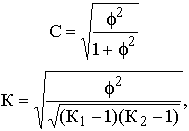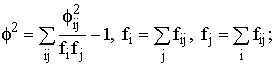какой метод используется для количественной оценки силы воздействия одних факторов на другие
Какой метод используется для выявления формы воздействия одних факторов на другие?
а) корреляционный анализ;
+б) регрессионный анализ;
в) индексный анализ;
г) дисперсионный анализ.
99. Какой метод используется для количественной оценки силы воздействия одних факторов на другие:
+а) корреляционный анализ;
б) регрессионный анализ;
в) метод средних величин;
г) дисперсионный анализ.
100. Какие показатели по своей величине существуют в пределах от минус до плюс единицы:
а) коэффициент детерминации;
б) корреляционной отношение;
+в) линейный коэффициент корреляции.
101. Коэффициент регрессии при однофакторной модели показывает:
+а) на сколько единиц изменяется функция при изменении аргумента на одну единицу;
б) на сколько процентов изменяется функция на одну единицу изменения аргумента.
102. Коэффициент эластичности показывает:
а) на сколько процентов изменяется функция с изменением аргумента на одну единицу своего измерения;
+б) на сколько процентов изменяется функция с изменением аргумента на 1%;
в) на сколько единиц своего измерения изменяется функция с изменением аргумента на 1%.
105. Величина индекса корреляции, равная 0,087, свидетельствует:
+а) о слабой их зависимости;
б) о сильной взаимосвязи;
в) об ошибках в вычислениях.
107. Величина парного коэффициента корреляции, равная 1,12, свидетельствует:
а) о слабой их зависимости;
б) о сильной взаимосвязи;
+в) об ошибках в вычислениях.
109. Какие из приведенных чисел могут быть значениями парного коэффициента корреляции:
111. Какие из приведенных чисел могут быть значениями множественного коэффициента корреляции:
115. Отметьте правильную форму линейного уравнения регрессии:
а) ŷ 
б) ŷ 
в) ŷ 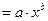
+г) ŷ 
119. Отметьте правильную форму параболической функции:
а) ŷ 
б) ŷ 
в) ŷ 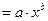
+г) ŷ 
120. Оценка статистической значимости парного коэффициента корреляции основывается:
+а) На использовании t – статистики;
б) На использовании F – статистики;
в) На использовании 
г) На графическом анализе остатков;
д) Дисперсионном анализе остатков.
121. Уравнение регрессии по рядам динамики можно построить:
+а) по первым разностям, по отклонениям от тренда, по уровням ряда с включением фактора времени;
б) только по смешанным трендово-факторным моделям;
в) по первым разностям, по отклонениям от тренда.
122.Временной ряд – это:
+а) последовательность упорядоченных во времени числовых показателей, характеризующих уровень состояния и изменения изучаемого явления;
б) последовательность числовых показателей, характеризующих уровень состояния и изменения изучаемого явления;
в) последовательность упорядоченных временных интервалов, или моментов времени.
123. При каком значении средней относительной ошибки по модулю модель имеет высокую точность:
+а) обнаружения автокорреляции в остатках;
б) обнаружения циклической составляющей;
в) для проверки подчинения случайного компонента нормальному закону распределения.
125. Система рекурсивных уравнений:
а) когда каждая зависимая переменная x рассматривается как функция одного и того же результативного признака y;
б) когда каждая зависимая переменная y рассматривается как функция одного и того же набора факторов x;
в) когда каждая независимая переменная x рассматривается как функция одного и того же результативного признака y;
+г) когда в каждом последующем уравнении системы зависимая переменная представляет функцию от всех зависимых и независимых переменных предшествующих уравнений.
126. Какой критерий используется для проверки статистической значимости уравнения регрессии:
+а) F – критерий Фишера
б) t – критерий Стьюдента
в)
127. Система независимых уравнений:
а) когда каждая зависимая переменная x рассматривается как функция одного и того же результативного признака y;
+б) когда каждая зависимая переменная y рассматривается как функция одного и того же набора факторов x;
в) когда каждая независимая переменная x рассматривается как функция одного и того же результативного признака y;
г) когда в каждом последующем уравнении системы зависимая переменная представляет функцию от всех зависимых и независимых переменных.
128. Для выявления основной тенденции развития явления используются:
+а) метод укрупнения интервалов;
+б) метод скользящей средней;
г) расчет средней гармонической;
+д) аналитическое выравнивание.
129. Ряд динамики характеризует:
а) структуру совокупности по какому-либо признаку;
+б) изменение значений признака во времени;
в) определенное значение варьирующего признака в совокупности;
г) факторы изменения показателя на определенную дату или за определенный период.
130. Периодические колебания, возникающие под влиянием смены времени года называются…:
131. Автокорреляцией в статистике называется:
а) зависимость вариации значений одного показателя от вариации значений другого;
б) зависимость между цепными уровнями;
в) отклонения от тенденции;
+г) зависимость последующего уровня динамического ряда от предыдущего.
132. Критерий Дарбина-Уотсона служит для:
а) проверки наличия тенденции в ряду динамики;
б) проверки гипотезы о нормальном характере распределения ряда отклонений от тренда;
+в) обнаружения автокорреляции;
г) проверки адекватности прогноза по уравнению тренда.
133. Виды эконометрических систем:
+а) система независимых уравнений;
+б) система рекурсивных уравнений;
+в) система взаимозависимых уравнений;
г) система нормальных уравнений.
134. Составляющие ряда динамики:
Какой метод используется для количественной оценки силы воздействия одних факторов на другие
Глава 8. Статистическое изучение взаимосвязей
8.1. Основные понятия корреляционного и регрессионного анализа
Исследуя природу, общество, экономику, необходимо считаться со взаимосвязью наблюдаемых процессов и явлений. При этом полнота описания так или иначе определяется количественными характеристиками причинно-следственных связей между ними. Оценка наиболее существенных из них, а также воздействия одних факторов на другие является одной из основных задач статистики.
Формы проявления взаимосвязей весьма разнообразны. В качестве двух самых общих их видов выделяют функциональную (полную) и корреляционную (неполную) связи. В первом случае величине факторного признака строго соответствует одно или несколько значений функции. Достаточно часто функциональная связь проявляется в физике, химии. В экономике примером может служить прямо пропорциональная зависимость между производительностью труда и увеличением производства продукции.
Корреляционная связь (которую также называют неполной, или статистической) проявляется в среднем, для массовых наблюдений, когда заданным значениям зависимой переменной соответствует некоторый ряд вероятных значений независимой переменной. Объяснение тому – сложность взаимосвязей между анализируемыми факторами, на взаимодействие которых влияют неучтенные случайные величины. Поэтому связь между признаками проявляется лишь в среднем, в массе случаев. При корреляционной связи каждому значению аргумента соответствуют случайно распределенные в некотором интервале значения функции.
Например, некоторое увеличение аргумента повлечет за собой лишь среднее увеличение или уменьшение (в зависимости от направленности) функции, тогда как конкретные значения у отдельных единиц наблюдения будут отличаться от среднего. Такие зависимости встречаются повсеместно. Например, в сельском хозяйстве это может быть связь между урожайностью и количеством внесенных удобрений. Очевидно, что последние участвуют в формировании урожая. Но для каждого конкретного поля, участка одно и то же количество внесенных удобрений вызовет разный прирост урожайности, так как во взаимодействии находится еще целый ряд факторов (погода, состояние почвы и др.), которые и формируют конечный результат. Однако в среднем такая связь наблюдается – увеличение массы внесенных удобрений ведет к росту урожайности.
По направлению связи бывают прямыми, когда зависимая переменная растет с увеличением факторного признака, и обратными, при которых рост последнего сопровождается уменьшением функции. Такие связи также можно назвать соответственно положительными и отрицательными.
Относительно своей аналитической формы связи бывают линейными и нелинейными. В первом случае между признаками в среднем проявляются линейные соотношения. Нелинейная взаимосвязь выражается нелинейной функцией, а переменные связаны между собой в среднем нелинейно.
Существует еще одна достаточно важная характеристика связей с точки зрения взаимодействующих факторов. Если характеризуется связь двух признаков, то ее принято называть парной. Если изучаются более чем две переменные – множественной.
Указанные выше классификационные признаки наиболее часто встречаются в статистическом анализе. Но кроме перечисленных различают также непосредственные, косвенные и ложные связи. Собственно, суть каждой из них очевидна из названия. В первом случае факторы взаимодействуют между собой непосредственно. Для косвенной связи характерно участие какой-то третьей переменной, которая опосредует связь между изучаемыми признаками. Ложная связь – это связь, установленная формально и, как правило, подтвержденная только количественными оценками. Она не имеет под собой качественной основы или же бессмысленна.
По силе различаются слабые и сильные связи. Эта формальная характеристика выражается конкретными величинами и интерпретируется в соответствии с общепринятыми критериями силы связи для конкретных показателей.
В наиболее общем виде задача статистики в области изучения взаимосвязей состоит в количественной оценке их наличия и направления, а также характеристике силы и формы влияния одних факторов на другие. Для ее решения применяются две группы методов, одна из которых включает в себя методы корреляционного анализа, а другая – регрессионный анализ. В то же время ряд исследователей объединяет эти методы в корреляционно-регрессионный анализ, что имеет под собой некоторые основания: наличие целого ряда общих вычислительных процедур, взаимодополнения при интерпретации результатов и др.
Поэтому в данном контексте можно говорить о корреляционном анализе в широком смысле – когда всесторонне характеризуется взаимосвязь. В то же время выделяют корреляционный анализ в узком смысле – когда исследуется сила связи – и регрессионный анализ, в ходе которого оцениваются ее форма и воздействие одних факторов на другие.
Задачи собственно корреляционного анализа сводятся к измерению тесноты связи между варьирующими признаками, определению неизвестных причинных связей и оценке факторов оказывающих наибольшее влияние на результативный признак.
Задачи регрессионного анализа лежат в сфере установления формы зависимости, определения функции регрессии, использования уравнения для оценки неизвестных значении зависимой переменной.
Решение названных задач опирается на соответствующие приемы, алгоритмы, показатели, применение которых дает основание говорить о статистическом изучении взаимосвязей.
Следует заметить, что традиционные методы корреляции и регрессии широко представлены в разного рода статистических пакетах программ для ЭВМ. Исследователю остается только правильно подготовить информацию, выбрать удовлетворяющий требованиям анализа пакет программ и быть готовым к интерпретации полученных результатов. Алгоритмов вычисления параметров связи существует множество, и в настоящее время вряд ли целесообразно проводить такой сложный вид анализа вручную. Вычислительные процедуры представляют самостоятельный интерес, но знание принципов изучения взаимосвязей, возможностей и ограничений тех или иных методов интерпретации результатов является обязательным условием исследования.
Методы оценки тесноты связи подразделяются на корреляционные (параметрические) и непараметрические. Параметрические методы основаны на использовании, как правило, оценок нормального распределения и применяются в случаях, когда изучаемая совокупность состоит из величин, которые подчиняются закону нормального распределения. На практике это положение чаще всего принимается априори. Собственно, эти методы – параметрические – и принято называть корреляционными.
Непараметрические методы не накладывают ограничений на закон распределения изучаемых величин. Их преимуществом является и простота вычислений.
8.2. Парная корреляция и парная линейная регрессия
Простейшим приемом выявления связи между двумя признаками является построение корреляционной таблицы:
| \ Y \ X \ | Y1 | Y2 | . | Yz | Итого | Yi |
| X1 | f11 | 12 | . | f1z | 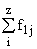 | 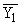 |
| X1 | f21 | 22 | . | f2z | 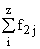 | 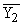 |
| . | . | . | . | . | . | . |
| Xr | fk1 | k2 | . | fkz | 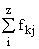 | 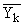 |
| Итого | 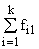 | 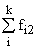 | . | 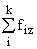 | n | 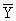 |
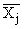 | 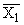 | 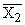 | . | 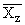 | 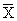 | — |
В основу группировки положены два изучаемых во взаимосвязи признака – Х и У. Частоты fij показывают количество соответствующих сочетаний Х и У. Если fij расположены в таблице беспорядочно, можно говорить об отсутствии связи между переменными. В случае образования какого-либо характерного сочетания fij допустимо утверждать о связи между Х и У. При этом, если fij концентрируется около одной из двух диагоналей, имеет место прямая или обратная линейная связь.
Наглядным изображением корреляционной таблице служит корреляционное поле. Оно представляет собой график, где на оси абсцисс откладывают значения Х, по оси ординат – У, а точками показывается сочетание Х и У. По расположению точек, их концентрации в определенном направлении можно судить о наличии связи.
В итогах корреляционной таблицы по строкам и столбцам приводятся два распределения – одно по X, другое по У. Рассчитаем для каждого Хi среднее значение У, т.е. 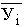
Последовательность точек (Xi, 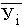
По существу, и корреляционная таблица, и корреляционное поле, и эмпирическая линия регрессии предварительно уже характеризуют взаимосвязь, когда выбраны факторный и результативный признаки и требуется сформулировать предположения о форме и направленности связи. В то же время количественная оценка тесноты связи требует дополнительных расчетов.
Практически для количественной оценки тесноты связи широко используют линейный коэффициент корреляции. Иногда его называют просто коэффициентом корреляции. Если заданы значения переменных Х и У, то он вычисляется по формуле
Можно использовать и другие формулы, но результат должен быть одинаковым для всех вариантов расчета.
Для характеристики влияния изменений Х на вариацию У служат методы регрессионного анализа. В случае парной линейной зависимости строится регрессионная модель
где n – число наблюдений;
а0, а1 – неизвестные параметры уравнения;
ei – ошибка случайной переменной У.
Уравнение регрессии записывается как
где Уiтеор – рассчитанное выравненное значение результативного признака после подстановки в уравнение X.
Параметры а0 и а1 оцениваются с помощью процедур, наибольшее распространение из которых получил метод наименьших квадратов. Его суть заключается в том, что наилучшие оценки ag и а, получают, когда
т.е. сумма квадратов отклонений эмпирических значений зависимой переменной от вычисленных по уравнению регрессии должна быть минимальной. Сумма квадратов отклонений является функцией параметров а0 и а1. Ее минимизация осуществляется решением системы уравнений
Можно воспользоваться и другими формулами, вытекающими из метода наименьших квадратов, например:
Аппарат линейной регрессии достаточно хорошо разработан и, как правило, имеется в наборе стандартных программ оценки взаимосвязи для ЭВМ. Важен смысл параметров: а1 – это коэффициент регрессии, характеризующий влияние, которое оказывает изменение Х на У. Он показывает, на сколько единиц в среднем изменится У при изменении Х на одну единицу. Если а, больше 0. то наблюдается положительная связь. Если а имеет отрицательное значение, то увеличение Х на единицу влечет за собой уменьшение У в среднем на а1. Параметр а1 обладает размерностью отношения У к X.
Параметр a0 – это постоянная величина в уравнении регрессии. На наш взгляд, экономического смысла он не имеет, но в ряде случаев его интерпретируют как начальное значение У.
Например, по данным о стоимости оборудования Х и производительности труда У методом наименьших квадратов получено уравнение
Коэффициент а, означает, что увеличение стоимости оборудования на 1 млн руб. ведет в среднем к росту производительности труда на 2.08 тыс. руб.
Значение функции У = a0 + а1Х называется расчетным значением и на графике образует теоретическую линию регрессии.
Смысл теоретической регрессии в том, что это оценка среднего значения переменной У для заданного значения X.
Парная корреляция или парная регрессия могут рассматриваться как частный случай отражения связи некоторой зависимой переменной, с одной стороны, и одной из множества независимых переменных – с другой. Когда же требуется охарактеризовать связь всего указанного множества независимых переменных с результативным признаком, говорят о множественной корреляции или множественной регрессии.
8.3. Оценка значимости параметров взаимосвязи
Получив оценки корреляции и регрессии, необходимо проверить их на соответствие истинным параметрам взаимосвязи.
Существующие программы для ЭВМ включают, как правило, несколько наиболее распространенных критериев. Для оценки значимости коэффициента парной корреляции рассчитывают стандартную ошибку коэффициента корреляции:
В первом приближении нужно, чтобы 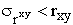
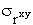
где tрасч – так называемое расчетное значение t-критерия.
Если tрасч больше теоретического (табличного) значения критерия Стьюдента (tтабл) для заданного уровня вероятности и (n-2) степеней свободы, то можно утверждать, что rxy значимо.
Подобным же образом на основе соответствующих формул рассчитывают стандартные ошибки параметров уравнения регрессии, а затем и t-критерии для каждого параметра. Важно опять-таки проверить, чтобы соблюдалось условие tрасч > tтабл. В противном случае доверять полученной оценке параметра нет оснований.
Вывод о правильности выбора вида взаимосвязи и характеристику значимости всего уравнения регрессии получают с помощью F-критерия, вычисляя его расчетное значение:
где n – число наблюдений;
m – число параметров уравнения регрессии.
Fрасч также должно быть больше Fтеор при v1 = (m-1) и v2 = (n-m) степенях свободы. В противном случае следует пересмотреть форму уравнения, перечень переменных и т.д.
8.4. Непараметрические методы оценки связи
Методы корреляционного и дисперсионного анализа не универсальны: их можно применять, если все изучаемые признаки являются количественными. При использовании этих методов нельзя обойтись без вычисления основных параметров распределения (средних величин, дисперсий), поэтому они получили название параметрических методов.
Между тем в статистической практике приходится сталкиваться с задачами измерения связи между качественными признаками, к которым параметрические методы анализа в их обычном виде неприменимы. Статистической наукой разработаны методы, с помощью которых можно измерить связь между явлениями, не используя при этом количественные значения признака, а значит, и параметры распределения. Такие методы получили название непараметрических.
Если изучается взаимосвязь двух качественных признаков, то используют комбинационное распределение единиц совокупности в форме так называемых таблиц взаимной сопряженности.
Рассмотрим методику анализа таблиц взаимной сопряженности на конкретном примере социальной мобильности как процесса преодоления замкнутости отдельных социальных и профессиональных групп населения. Ниже приведены данные о распределении выпускников средних школ по сферам занятости с выделением аналогичных общественных групп их родителей.
| Занятия родителей | Число детей, занятых в | Всего | |||
| Промышлен- ности и стро- ительстве | сельском хозяйстве | сфере обслужи- вания | сфере интел- лектуального труда | ||
| 1. Промышленность и строительство 2. Сельское хозяйство 3. Сфера обслуживания 4. Сфера интеллектульного труда | 40 34 16 24 | 5 29 6 5 | 7 13 15 9 | 39 12 19 72 | 91 88 56 110 |
| Всего | 114 | 45 | 44 | 142 | 345 |
Распределение частот по строкам и столбцам таблицы взаимной сопряженности позволяет выявить основные закономерности социальной мобильности: 42,9 % детей родителей группы 1 («Промышленность и строительство») заняты в сфере интеллектуального труда (39 из 91); 38,9 % детей. родители которых трудятся в сельском хозяйстве, работают в промышленности (34 из 88) и т.д.
Можно заметить и явную наследственность в передаче профессий. Так, из пришедших в сельское хозяйство 29 человек, или 64,4 %, являются детьми работников сельского хозяйства; более чем у 50 % в сфере интеллектуального труда родители относятся к той же социальной группе и т.д.
Однако важно получить обобщающий показатель, характеризующий тесноту связи между признаками и позволяющий сравнить проявление связи в разных совокупностях. Для этой цели исчисляют, например, коэффициенты взаимной сопряженности Пирсона (С) и Чупрова (К):
где f 2 – показатель средней квадратической сопряженности, определяемый путем вычитания единицы из суммы отношений квадратов частот каждой клетки корреляционной таблицы к произведению частот соответствующего столбца и строки:
К1 и К2 – число групп по каждому из признаков. Величина коэффициента взаимной сопряженности, отражающая тесноту связи между качественными признаками, колеблется в обычных для этих показателей пределах от 0 до 1.
В социально-экономических исследованиях нередко встречаются ситуации, когда признак не выражается количественно, однако единицы совокупности можно упорядочить. Такое упорядочение единиц совокупности по значению признака называется ранжированием. Примерами могут быть ранжирование студентов (учеников) по способностям, любой совокупности людей по уровню образования, профессии, по способности к творчеству и т.д.
При ранжировании каждой единице совокупности присваивается ранг, т.е. порядковый номер. При совпадении значения признака у различных единиц им присваивается объединенный средний порядковый номер. Например, если у 5-й и 6-й единиц совокупности значения признаков одинаковы, обе получат ранг, равный (5 + 6) / 2 = 5,5.
Измерение связи между ранжированными признаками производится с помощью ранговых коэффициентов корреляции Спирмена (r) и Кендэлла (t). Эти методы применимы не только для качественных, но и для количественных показателей, особенно при малом объеме совокупности, так как непараметрические методы ранговой корреляции не связаны ни с какими ограничениями относительно характера распределения признака.