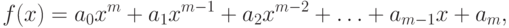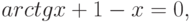какой метод численного решения уравнений может найти все корни уравнения если их больше одного

Вычислительная математика копия 1

Уравнение называется алгебраическим, если его можно представить в виде:

Формула (1.1) – каноническая форма записи алгебраического уравнения. Если уравнение f(x)=0 не удается привести к виду (1.1) заменой переменных, то уравнение называется трансцендентным.

Известно, что уравнение (1.1) имеет ровно n корней – вещественных или комплексных. Если n =1, 2, 3 [и иногда 4 (биквадратное уравнение], то существуют точные методы решения уравнения (1.1). Если же n >4 или уравнение – трансцендентное, то таких методов не существует, и решение уравнения ищут приближенными методами. Всюду при дальнейшем изложении будем предполагать, что f(x) – непрерывная функция. Методы, которые мы рассмотрим, пригодны для поиска некратных (то есть изолированных) корней.

1.1 Отделение корня

Решение уравнения состоит из двух этапов: 1 – отделение корня, 2 – его уточнение.

Корень можно отделить аналитически и графически.

Графический метод отделения корня

1.2 Уточнение корня методом деления отрезка пополам

Самый простой метод, пригодный для любых непрерывных функций – метод деления отрезка пополам.

1.3 Метод хорд

Источник

Численные методы решения систем нелинейных уравнений

Введение

Многие прикладные задачи приводят к необходимости нахождения общего решения системы нелинейных уравнений. Общего аналитического решения системы нелинейных уравнений не найдено. Существуют лишь численные методы.

Следует отметить интересный факт о том, что любая система уравнений над действительными числами может быть представлена одним равносильным уравнением, если взять все уравнения в форме , возвести их в квадрат и сложить.

Для численного решения применяются итерационные методы последовательных приближений (простой итерации) и метод Ньютона в различных модификациях. Итерационные процессы естественным образом обобщаются на случай системы нелинейных уравнений вида:

(1)

Обозначим через вектор неизвестных и определим вектор-функцию Тогда система (1) записывается в виде уравнения:

(2)

Теперь вернёмся к всеми любимому Python и отметим его первенство среди языков программирования, которые хотят изучать [1].

Этот факт является дополнительным стимулом рассмотрения числительных методов именно на Python. Однако, среди любителей Python бытует мнение, что специальные библиотечные функции, такие как scipy.optimize.root, spsolve_trianular, newton_krylov, являются самым лучшим выбором для решения задач численными методами.

С этим трудно не согласится хотя бы потому, что в том числе и разнообразие модулей подняло Python на вершину популярности. Однако, существуют случаи, когда даже при поверхностном рассмотрении использование прямых известных методов без применения специальных функций библиотеки SciPy тоже дают неплохие результаты. Иными словами, новое- это хорошо забытое старое.

Так, в публикации [2], на основании проведенных вычислительных экспериментов, доказано, что библиотечная функция newton_krylov, предназначенная для решения больших систем нелинейных уравнений, имеет в два раза меньшее быстродействие, чем алгоритм TSLS+WD
(two-step least squares), реализованный средствами библиотеки NumPy.

Целью настоящей публикации является сравнение по числу итераций, быстродействию, а главное, по результату решения модельной задачи в виде системы из ста нелинейных алгебраических уравнений при помощи библиотечной функции scipy.optimize.root и методом Ньютона, реализованного средствами библиотеки NumPy.

Возможности решателя scipy.optimize.root для численного решения систем алгебраических нелинейных уравнений

Библиотечная функция scipy.optimize.root выбрана в качестве базы сравнения, потому что имеет обширную библиотеку методов, пригодных для сравнительного анализа.

scipy.optimize.root(fun, x0, args=(), method=’hybr’, jac=None, tol=None,callback=None, ptions=None)
fun — Векторная функция для поиска корня.
x0 –Начальные условия поиска корней

Методы решения систем нелинейных уравнений

Приведенный далее материал действительно можно прочитать в литературе, например в [4], но я уважаю своего читателя и для его удобства приведу вывод метода по возможности в сокращенном виде. Те, кто не любит формулы, этот раздел пропускают.

В методе Ньютона новое приближение для решения системы уравнений (2) определяется из решения системы линейных уравнений:

(3)

Определим матрицу Якоби:

(4)

(5)

Многие одношаговые методы для приближенного решения (2) по аналогии с двухслойными итерационными методами для решения систем линейных алгебраических уравнений можно записать в виде:

(6)

где — итерационные параметры, a — квадратная матрица n х n, имеющая обратную.

При использовании записи (6) метод Ньютона (5) соответствует выбору:

Система линейных уравнений (5) для нахождения нового приближения может решаться итерационно. В этом случае мы имеем двухступенчатый итерационный процесс с внешними и внутренними итерациями. Например, внешний итерационный процесс может осуществляться по методу Ньютона, а внутренние итерации — на основе итерационного метода Зейделя

При решении систем нелинейных уравнений можно использовать прямые аналоги стандартных итерационных методов, которые применяются для решения систем линейных уравнений. Нелинейный метод Зейделя применительно к решению (2) дает:

(7)

В этом случае каждую компоненту нового приближения из решения нелинейного уравнения, можно получить на основе метода простой итерации и метода Ньютона в различных модификациях. Тем самым снова приходим к двухступенчатому итерационному методу, в котором внешние итерации проводятся в соответствии с методом Зейделя, а внутренние — с методом Ньютона.

Основные вычислительные сложности применения метода Ньютона для приближенного решения систем нелинейных уравнений связаны с необходимостью решения линейной системы уравнений с матрицей Якоби на каждой итерации, причем от итерации к итерации эта матрица меняется. В модифицированном методе Ньютона матрица Якоби обращается только один раз:

(8)

Выбор модельной функции

Такой выбор не является простой задачей, поскольку при увеличении числа уравнений в системе в соответствии с ростом числа переменных результат решения не должен меняться, поскольку в противном случае невозможно отследить правильность решения системы уравнений при сравнении двух методов. Привожу следующее решение для модельной функции:

Функция f создаёт систему из n нелинейных уравнений, решение которой не зависит от числа уравнений и для каждой из n переменных равно единице.

Программа для тестирования на модельной функции c результатами решения системы алгебраических нелинейных уравнений с помощью библиотечной функции optimize.root для разных методов отыскания корней

Только один из методов, приведенных в документации [3] прошёл тестирование по результату решения модельной функции, это метод ‘krylov’.

Solution:
[1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1.
1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1.
1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1.
1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1.
1. 1. 1. 1.]
Krylov method iteration = 4219
Optimize root time 7.239 seconds:

Вывод: С увеличением числа уравнений вдвое заметно появление ошибок в решении. При дальнейшем увеличении n решение становится не приемлемым, что возможно из-за автоматической адаптации к шагу, эта же причина резкого падения быстродействия. Но это только моё предположение.

Программа для тестирования на модельной функции c результатами решения системы алгебраических нелинейных уравнений с помощью программы написанной на Python 3 с учётом соотношений (1)-(8) для отыскания корней по модифицированному методу Ньютона

Solution:
[1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1.
1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1.
1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1.
1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1.
1. 1. 1. 1.]
Newton iteration = 13
Newton method time 0.496 seconds

Solution:
[1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1.
1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1.
1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1.
1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1.
1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1.
1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1.
1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1.
1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1.
1. 1. 1. 1. 1. 1. 1. 1.]
Newton iteration = 14
Newton method time 1.869 seconds

Чтобы убедиться в том, что программа действительно решает систему, перепишем модельную функцию для ухода от корня со значением 1 в виде:

Вывод: Программа работает и при изменении модельной функции.

Теперь вернёмся к начальной модельной функции и проверим более широкий диапазон для n, например в 2 и 500.
n=2
Solution:
[1. 1.]
Newton iteration = 6
Newton method time 0.048 seconds
n=500

Источник

Численные методы решения уравнений

Доказано также, что не имеют аналитического решения алгебраические уравнения степени выше четвертой:

Для поиска корней таких уравнений используются численные (приближенные) методы, которые по своей сути являются способами уточнения корней 5.

В общем случае запись нелинейного уравнения имеет вида

Задача решения нелинейного уравнения состоит из двух этапов:

1) локализация корней, т.е. определение интервала изоляции (интервала неопределенности), в котором расположен корень;

2) определение с заданной точностью точности ε приближенного значения корня.

Для локализации корней можно воспользоваться следующей теоремой.

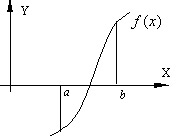
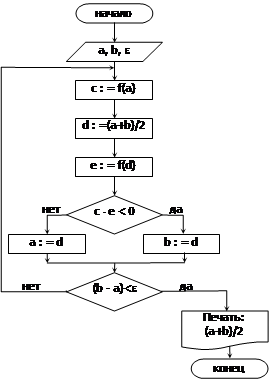
Теорема: Если непрерывная функция y=f(x) на концах отрезка [a, b] принимает значения разных знаков, т.е. f(a)·f(b)

и вычисляется значение функции f(d).

Далее делается выбор, какую из двух частей отрезка взять для дальнейшего уточнения корня. Для чего проверяется условие

Блок-схема метода половинного деления представлена на рисунке 12.

Метод хорд

Идея метода хорд заключается в том, что кривая y=f(x) на участке [a, b] заменяется хордой и в качестве приближенного значения корня х * =x_n принимается точка пересечения оси абсцисс с хордой (рисунок 13).

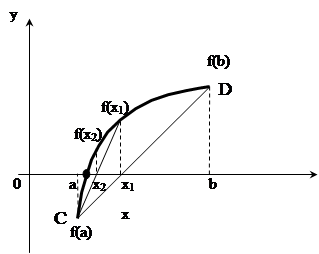Рисунок 13 – Графическая интерпретация метода хорд

Запишем уравнение хорды, проходящей через точки С с координатами (a, f(a)) и D – (b, f(b)):

.

Абсцисса точки пересечения хорды с осью ОХ находится из этого выражения при y=0, т.е.

.

Выполнив преобразования, получаем выражение для нахождения приближенного корня:

. (35)

Если значения функции при х=а и х=x_n имеют разные знаки, т.е. выполняется условие

Вычисления повторяются до тех пор, пока выполняется условие

Блок-схема, реализующая метод хорд, приведена на рисунке 14.

Метод Ньютона (метод касательных)

Этот метод основан на замене функции y=f(x) в точке начального приближения x=x₀ касательной, пересечение которой с осью х дает первое приближение корня х₁ и т.д. (рисунок 15).

В качестве x₀ выбирают тот конец отрезка [a, b] (т.е. точку С или точку D), для которого выполняется условие:

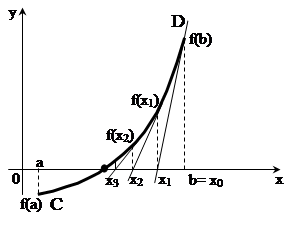Рисунок 15 – Графическая интерпретация метода Ньютона

Для графической иллюстрации (рисунок 15), где начальное приближение находится в точке D, т.е. x₀=b, запишем:

,

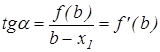
откуда 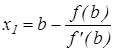или .

Тогда, в общем виде выражение для нахождения корня можно записать:

Итерационный процесс уточнения корня выполняется до тех пор, пока соблюдается условие

Блок-схема, реализующая метод Ньютона, приведена на рисунке 16.

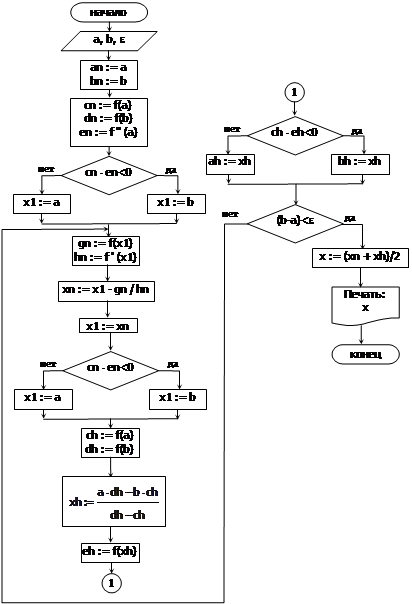
Комбинированные методы

Комбинированные методы решения уравнения основаны на сочетании описанных выше методов и позволяют получить приближение к корню с противоположных сторон с сужением интервала локализации корня.

Оба метода используются последовательно, при этом интервал локализации сравнивается с заданной точностью e. Корень уравнения находится как среднее двух значений, полученных каждым из методов.

На рисунке 17 приведена блок-схема комбинированного метода хорд-Ньютона.

Источник

Численные методы решения нелинейных уравнений

Если законы функционирования модели нелинейны, а моделируемые процесс или система обладают одной степенью свободы (т.е. имеют одну независимую переменную), то такая модель, как правило, описывается одним нелинейным уравнением.

Необходимость отыскания корней нелинейных уравнений встречается в расчетах систем автоматического управления и регулирования, собственных колебаний машин и конструкций, в задачах кинематического анализа и синтеза, плоских и пространственных механизмов и других задачах.

Дано нелинейное уравнение:

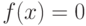( 4.1)

Необходимо решить это уравнение, т. е. найти его корень .

Если функция имеет вид многочлена степени m,

Такие уравнения обычно имеют бесконечное множество решений.

Доказано также, что нельзя построить формулу, по которой можно было бы решать произвольные алгебраические уравнения степени, выше четвертой.

Процесс определения корней алгебраических и трансцендентных уравнений состоит из 2 этапов:

Для алгебраических и трансцендентных уравнений пригодны одни и те же методы уточнения приближенных значений действительных корней:

Источник

Численное решение нелинейных уравнений с одной переменной

Информатика, 10-11 классы

, ДВГГУ

ЧИСЛЕННОЕ РЕШЕНИЕ НЕЛИНЕЙНЫХ УРАВНЕНИЙ С ОДНОЙ ПЕРЕМЕННОЙ

При решении задач прикладного характера в разнообразных разделах физики, механики, техники и других областях возникает необходимость решения нелинейных уравнений с одной переменной. При этом многие уравнения не имеют аналитических решений. Это относится к большинству трансцендентных уравнений. Также доказано, что нельзя построить формулу, по которой можно было бы решить произвольное алгебраические уравнение выше четвертой степени.

Уравнение будем называть линейным[1], алгебраическим или трансцендентным в зависимости от того, имеет ли оно одно решение, n решений или неопределенное число решений.

Нелинейные уравнения можно разделить на два класса – алгебраические и трансцендентные. Алгебраическими уравнениями называют уравнения, содержащие только алгебраические функции (целые, рациональные, иррациональные). Например, многочлен является целой алгебраической функцией. Уравнения, содержащие другие функции (тригонометрические, показательные, логарифмические и другие) называются трансцендентными.[2]

Методы решения нелинейных уравнений делятся на две группы:

Точные методы позволяют записать корни в виде некоторого конечного соотношения (формулы). Из школьного курса алгебры известны такие методы для решения тригонометрических, логарифмических, показательных, а также простейших алгебраических уравнений.

Далее будут рассмотрены несколько численных методов и приведены алгоритмы нахождения корней уравнений.

В общем случае нелинейное уравнение можно записать в виде:

(1)

(2)

где функции f(x) и g(x) также определены и непрерывны на интервале .

Всякое число обращающее уравнения (1) или (2) в верные числовые равенства называется корнем этого уравнения.

Корни уравнения могут быть действительными и комплексными. В дальнейшем будет идти речь только о вычислении действительных корней.

Решить уравнение численно значит:

1) установить имеет ли оно действительные корни;

2) отделить эти корни (то есть на числовой оси найти достаточно тесные промежутки, называемые интервалами изоляции корня, содержащие только один корень данного уравнения);

3) уточнить отделенные корни, т. е. найти значения корней с заданной степенью точности .

Последнее означает следующее.

Любое число, содержащееся между и , можно принять за приближенное значение корня x* с точностью до .

Графические методы решения уравнений[3]

Пусть дано уравнение F (х) = 0. Построим график функции F (х). Абсциссы точек пересечения графика с осью Ох и являются корнями уравнения. Иногда для графического решения уравнения удобнее записать его в виде и построить графики функций: и Абсциссы точек пересечения этих графиков и являются корнями уравнения F (х) = 0 (рис. 12).

Однако этот метод позволяет получить лишь грубо приближенные значения корней уравнения. Для получения значений корней с большей точностью применяются численные методы. Однако, графи­ческий метод очень удобен, так как он позволяет найти корни с точностью, достаточной для решения многих практических задач, а также достаточно нагляден, прост и доступен.

Численные методы решения уравнений

Наиболее распространенными на практике численными методами решения уравнения (1) являются: метод половинного деления, метод хорд, метод касательных, метод простой итерации и т. д.[4]

Процесс численного решения уравнений разбивается на три этапа:

1. Отделение корней уравнения. Этот процесс можно сделать как графически, так и аналитически. Важно найти такие отрезки, которые бы содержали по одному корню уравнения (1).

2. Выбор метода решения и преобразование уравнения к виду, удобному для применения данного метода.

3. Уточнение корней с заданной точностью при помощи выбранного численного метода.

Говорят, что корень x* уравнения отделен на отрезке , если он содержится в данном отрезке, и если на этом отрезке других корней нет.

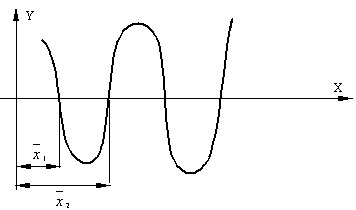
Провести полное отделение всех корней уравнения – значит разбить всю область допустимых значений на интервалы (или на отрезки), в каждом из которых содержится ровно по одному корню (или не содержится ни одного корня).

Отделение корней обычно начинают проводить графически. Для этого строят графики функций, получают интервалы, в которых на­ходятся корни уравнения. Это предположение затем проверяют ана­литически, пользуясь следующим свойством непрерывной функции F(x): если функция непрерывна на интервале и на его концах имеет разные знаки (), то между точками a и b имеется хотя бы один корень уравнения . При этом корней может оказаться и несколько, как показано на рис. 13.

Для того чтобы на интервале существовал только один корень, должно выполняться следующее свойство: если функция непрерывна и монотонна на отрезке и принимает на концах отрезка значения разных знаков, то внутри отрезка содержится корень уравнения и этот корень единственный (рис. 14, а, b).

Пример 1: Отделить графически положительные корни уравнения

Решение: Найдем приближенные значения корней уравнения графически. Для этого удобно представить уравнение в следующем виде: e0,3x = 2 sin(2x).

Решением данного уравнения будет являться абсцисса x точки пересечения графиков следующих функций: y1(x) = 2 sin(2x);

На рисунке видно, что графики функций y1(x) и y2(x) пересекаются в двух точках A и B, абсциссы которых положительны и лежат соответственно в промежутках и. Следовательно, уравнение имеет два положительных корня x1 и x2, которые лежат в промежутках и.

Примечание: Графики функций можно строить с помощью компьютера, например, в электронных таблицах Excel или в MathCad.

Пример 2: Отделить аналитически корни уравнения

x3 – 3x2 + 11x + 1 = 0 (4)

Решение: Для аналитического отделения корней найдем производную функции

Производная этой функции

Из таблицы видно, что f(-1)f(0)

Источник