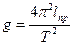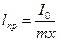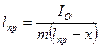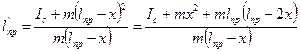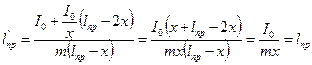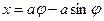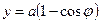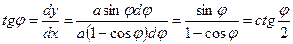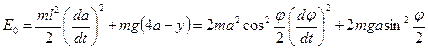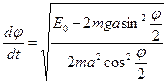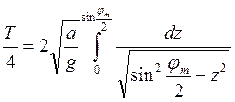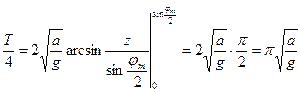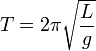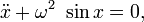какой маятник называется оборотным
Оборотный маятник



Важным примером практического применения физических маятников является так называемый оборотный маятник, служащий преимущественно для гравиметрической разведки, определения ускорения свободного падения в данной точке земной поверхности. Для достижения этой цели в процессе эксперимента маятник закрепляют так, чтобы его центр качания стал новой точкой подвеса и снова измеряют период колебаний. Если периоды колебаний маятника в обоих случаях одинаковы, значит равны и приведённые длины маятников в обоих случаях. Техника измерения длин высока, поэтому, измеряя расстояние между точками подвеса в двух положениях маятника, можно с высокой степенью точности определить приведенную длину маятника, и измерив период само значение ускорения свободного падения:
Для определения ускорения свободного падения можно было бы, конечно, применить и математический маятник. Но приближения, которые мы применяем, считая физический маятник математическим, не могут обеспечить достаточно высокую точность измерений. Кроме того, в эксперименте весьма затруднительно определить положение центра масс тела маятника и расстояние до него от точки подвеса. Всё это приводит к тому, что для точных определений ускорения свободного падения необходимо считать маятник физическим, а это приводит к дополнительным трудностям.
Очень важным, с точки зрения гравиметрических измерения, является следующее свойство физического маятника: если заставить маятник колебаться относительно центра качания, то прежняя точка подвеса станет новым центром качания, иначе говоря, центр качания и точка подвеса обладают свойством сопряженности.
Определить положение центра качания расчётным путём затруднительно в реальных условиях эксперимента, соответственно, трудно с достаточной степенью точности определить приведённую длину маятника. Но, пользуясь указанным свойством физического маятника, можно очень точно определить расстояние между двумя точками маятника, периоды колебаний относительно которых равны между собой, т.е. определить приведённую длину. Докажем теперь, что если подвесить маятник в центре качания, то прежняя точка подвеса станет новым центром качания, т.е. приведённая длина маятника не изменится.
Если маятник подвешен в О, то приведённая длина его будет равна:
При повороте маятника и накоплении его в т. О’ приведённая длина становится:
По теореме Гюйгенса-Штейнера момент инерции маятника относительно оси, проходящей через О`, можно записать в виде 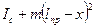
После несложных преобразований получаем, чть приведённая длина маятника одинакова в тех случаях, когда маятник колеблется относительно точек О’ и О, т.е. приведённая длина не изменяется:
измерив расстояние между точками подвеса маятника, для которых период принимает одинаковое значение, и измерив само значение периода колебаний, определим затем и ускорение свободного падения.
16.10. Циклоидальный маятник.
Математический и физический маятники имеют циклическую частоту и период, не зависящие от амплитуды колебаний только в том случае, когда амплитуда колебаний достаточно мала. С увеличением амплитуды колебаний они перестают быть, с одной стороны, гармоническими и, с другой стороны, их период будет уже зависеть от величины амплитуды. Однако, изменяя соответствующим образом параметры маятника, например, длину математического маятника, можно добиться того, что и при больших значениях амплитуды колебаний период колебаний не будет зависеть от её значения. Таким является так называемый циклоидальный маятник. Циклоидальным называют обычно математический маятник, у которого тело движется под действием силы тяжести по дуге циклоиды, ось которой вертикальна, а выпуклость обращена вниз. Период колебаний циклоидального маятника не зависит от амплитуды и определяется формулой
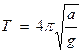
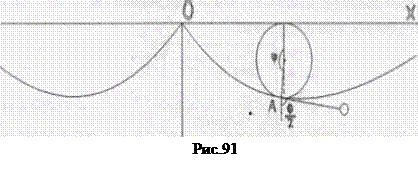
Таким образом, для циклоидального маятника строго выполняется свойство изохронности колебаний. На рис. 91 приведена разновидность циклоидального маятника, отличающаяся от приведенного его определения тем, что нить математического маятника при его колебаниях касается циклоиды, т.е. длина математического маятника с ростом отклонения тела от положения равновесия уменьшается на соответствующую дугу циклоиды.
 |
Положим, что радиус круга, образующего циклоиду, равен а, а длина маятника 4a. Уравнение циклоиды тогда можно записать в виде
где угол 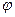
При колебаниях маятника в любой момент времени его длина уменьшается на величину дуги циклоиды, которой в этот момент времени касается нить маятника. Нить направлена по касательной к циклоиде в т. А. Тангенс угла отклонения нити от положительного направления оси ОХ легко определяется из выражения:
Отсюда видно, что угол отклонения нити маятника от вертикали равен 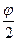
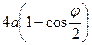
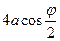
Предположим далее, что колебания маятника возбуждаются толчком, т.е. ему сообщается кинетическая энергия. При максимальном отклонении тела маятника от положения равновесия при отсутствии сил сопротивления движению энергия его полностью переходит в потенциальную энергию в поле тяготения, т.е. 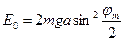
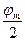
В произвольный момент времени полная энергия маятника (см. «Энергия колебательного движения») состоит из кинетической энергии движения и потенциальной энергии в поле силы тяжести:
Из полученного выражения для закона сохранения энергии получим значение угловой скорости маятника для произвольного момента времени
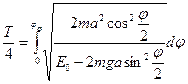 |
Последнее выражение позволяет определить период колебаний маятника. Действительно, время движения маятника от положения равновесия до максимального отклонения равно четверти периода, поэтому
Выражение интеграла можно привести к более удобному для интегрирования виду, учитывая значение кинетической энергии, сообщённой маятнику
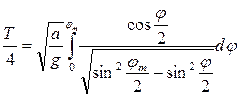 |
Если применить подстановку 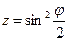
После интегрирования получаем
Следовательно, период колебаний циклоидального маятника совершенно не зависит от амплитуды колебаний, т.е. свойство изохронности колебаний выполняется строго. Значение периода колебаний будет определяться только параметрами самой циклоиды (радиусом круга, образующего циклоиду):
Большая Энциклопедия Нефти и Газа
Оборотный маятник
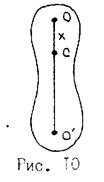
Оборотный маятник представляет собой пластину с прорезью, снабженную двумя трехгранными ножами, острые ребра которых О и Oi расположены так, что могут по очереди служить осями вращения. Ножи прикреплены к пластине таким образом, что лезвия ножей ( фиг. [1]
Оборотным маятником называется физический маятник, центр качаний которого расположен в пределах колеблющегося тела. [2]
Такую форму дают оборотному маятнику с тою целью, чтобы сопротивление воздуха при качаниях его в обоих положениях было одинаково. [5]
Расстояние между остриями ножей оборотного маятника может быть измерено весьма точно при помощи компаратора. Поэтому для абсолютных измерений напряжения силы тяжести оборотный маятник вполне заменяет нам идеальный, которого в действительности, конечно, построить нельзя. [7]
Теорема Гюйгенса используется в оборотном маятнике для точных измерений ускорения свободного падения. Существуют разнообразные конструкции оборотного маятника. [8]
Таким образом, при помощи оборотного маятника экспериментально определяется ускорение свободного падения на земной поверхности, и, в частности, обнаруживаются аномалии, свидетельствующие о залегании полезных ископаемых. [9]
Обе эти величины в методе оборотного маятника измеряются непосредственно. В основу этого метода положена теорема о сопряженности так называемого центра вращения и центра колебания физического маятника. Центром вращения называется точка подвеса, около которой колеблется физический маятник. [10]
При определении силы тяжести методом наблюдений оборотных маятников в наблюденное значение силы тяжести g приходится вносить целый ряд поправок для исключения различных погрешностей. Важнейшими источниками погрешностей являются: 1) колебания температуры во время наблюдений, 2) удлинение стержня маятника при помещении его в вакуум, 3) сокачанпе штатива, 4) влияние амплитуды, 5) отсутствие полного вакуума в вакуумной камере, 6) влияние суточного хода яасов, 7) влияние деформаций призм и подушек, на которых совершаются колебания маятника, и др. Точность этих определений весьма высока. [14]
ОБОРОТНЫЙ МАЯТНИК
Смотреть что такое ОБОРОТНЫЙ МАЯТНИК в других словарях:
ОБОРОТНЫЙ МАЯТНИК
прибор для экспериментального определения ускорения силы тяжести g. Представляет собой тело, например массивную пластину (рис.), с двумя трёхгр. смотреть
ОБОРОТНЫЙ МАЯТНИК
ОБОРОТНЫЙ МАЯТНИК, прибор для экспериментального определения ускорения силы тяжести д. Представляет собой тело, напр, массивную пластину (рис.), с дв. смотреть
ОБОРОТНЫЙ МАЯТНИК
физ. маятник, к-рый служит для определения ускорения свободного падения д. Имеет две параллельные оси подвеса, расстояние l между к-рыми изменяют, доби. смотреть
ОБОРОТНЫЙ МАЯТНИК
ОБОРОТНЫЙ МАЯТНИК, физический маятник, который служит для определения ускорения свободного падения g. Имеет две параллельные оси подвеса, расстояние h между которыми изменяют, добиваясь того, чтобы период колебаний Т около каждой из осей имел одинаковую величину. Зная Т и h, определяют g=4p2h/Т2.
ОБОРОТНЫЙ МАЯТНИК
ОБОРОТНЫЙ МАЯТНИК
ОБОРОТНЫЙ МАЯТНИК
ОБОРОТНЫЙ МАЯТНИК, физический маятник, который служит для определения ускорения свободного падения g. Имеет две параллельные оси подвеса, расстояние h между которыми изменяют, добиваясь того, чтобы период колебаний Т около каждой из осей имел одинаковую величину. Зная Т и h, определяют g=4p2h/Т2. смотреть
ОБОРОТНЫЙ МАЯТНИК
— физический маятник, который служит для определенияускорения свободного падения g. Имеет две параллельные оси подвеса,расстояние h между которыми изменяют, добиваясь того, чтобы периодколебаний Т около каждой из осей имел одинаковую величину. Зная Т и h,определяют g=4p2h/Т2. смотреть
ОБОРОТНЫЙ МАЯТНИК
(для измерения ускорений силы тяжести) Karter’s pendulum
Оборотный маятник
Смотреть что такое «Оборотный маятник» в других словарях:
ОБОРОТНЫЙ МАЯТНИК — прибор для эксперим. определения ускорения свободного падения g. Представляет собой тело, напр. массивную пластину (рис.) с двумя трёхгранными ножами, из к рых один неподвижен, а другой может перемещаться вдоль прорези на пластине. Острые рёбра… … Физическая энциклопедия
ОБОРОТНЫЙ МАЯТНИК — физический маятник, который служит для определения ускорения свободного падения g. Имеет две параллельные оси подвеса, расстояние h между которыми изменяют, добиваясь того, чтобы период колебаний Т около каждой из осей имел одинаковую величину.… … Большой Энциклопедический словарь
оборотный маятник — физический маятник, который служит для определения ускорения свободного падения g. Имеет две параллельные оси подвеса, расстояние l между которыми изменяют, добиваясь того, чтобы период колебаний T около каждой из осей имел одинаковую величину.… … Энциклопедический словарь
оборотный маятник — apverčiamoji svyruoklė statusas T sritis Standartizacija ir metrologija apibrėžtis Įtaisas laisvojo kritimo pagreičiui nustatyti. atitikmenys: angl. Kater’s pendulum; reversible pendulum vok. Reversionspendel, n; Umkehrpendel, n rus. оборотный… … Penkiakalbis aiškinamasis metrologijos terminų žodynas
оборотный маятник — apverčiamoji švytuoklė statusas T sritis fizika atitikmenys: angl. Kater’s pendulum; reversible pendulum vok. Reversionspendel, n; Umkehrpendel, n rus. оборотный маятник, m pranc. pendule réversible, m … Fizikos terminų žodynas
ОБОРОТНЫЙ МАЯТНИК — физ. маятник, к рый служит для определения ускорения свободного падения д. Имеет две параллельные оси подвеса, расстояние l между к рыми изменяют, добиваясь того, чтобы период колебаний T около каждой из осей имел одинаковую величину. Зная Т и l … Естествознание. Энциклопедический словарь
ОБОРОТНЫЙ — МАЯТНИК прибордля эксперим. определения ускорения свободного падения g. Представляетсобой физ. маятник в виде, напр., массивной пластины (рис.) с двумятрёхгранными ножами, из к рых один неподвижен, а другой может перемещатьсявдоль прорези на… … Физическая энциклопедия
Маятник — твёрдое тело, совершающее под действием приложенных сил колебания около неподвижной точки или оси. В физике под М. обычно понимают М., совершающий колебания под действием силы тяжести; при этом его ось не должна проходить через центр… … Большая советская энциклопедия
Маятник — М. называется тяжелое тело, совершающее колебания около неподвижной точки. Высокий интерес, представляемый движением М., замечен был впервые Галилеем, который усмотрел тесную связь между законами падения тел и законом качаний М. В 1657 г. Гюйгенс … Энциклопедический словарь Ф.А. Брокгауза и И.А. Ефрона
Маятники (математический, физический, оборотный).
Ма́ятник — система, подвешенная в поле тяжести и совершающая механические колебания. Колебания совершаются под действием силы тяжести, силы упругости и силы трения. Во многих случаях трением можно пренебречь, а от сил упругости (либо сил тяжести) абстрагироваться, заменив их связями.
Во время колебаний маятника происходят постоянные превращения энергии из одного вида в другой. Кинетическая энергия маятника превращается в потенциальную энергию (гравитационную, упругую) и обратно. Кроме того, постепенно происходит диссипация кинетической энергии в тепловую за счёт сил трения.
Одним из простейших маятников является шарик, подвешенный на нити. Идеализацией этого случая является математический маятник — механическая система, состоящая из материальной точки, подвешенной на невесомой нерастяжимой нити или на невесомом стержне в поле тяжести.
Если размерами массивного тела пренебречь нельзя, но всё еще можно не учитывать упругих колебаний тела, то можно прийти к понятию физического маятника. Физический маятник — твёрдое тело, совершающее колебания в поле каких-либо сил относительно точки, не являющейся центром масс этого тела, или неподвижной горизонтальной оси, не проходящей через центр масс этого тела.
Система из нескольких шариков, подвешенных на нитях в одной плоскости, колеблющихся в этой плоскости и соударяющихся друг с другом, называетсямаятником Ньютона. Здесь уже приходится учитывать упругие процессы.
Математи́ческий ма́ятник — осциллятор, представляющий собой механическую систему, состоящую из материальной точки, находящейся на невесомойнерастяжимой нити или на невесомом стержне в однородном поле сил тяготения. Период малых собственных колебаний математического маятника длины Lнеподвижно подвешенного в однородном поле тяжести с ускорением свободного падения g равен
и не зависит [2] от амплитуды колебаний и массы маятника.
Плоский математический маятник со стержнем — система с одной степенью свободы. Если же стержень заменить на растяжимую нить, то это система с двумя степенями свободы со связью. Пример школьной задачи, в которой важен переход от одной к двум степеням свободы.
При малых колебаниях физический маятник колеблется так же, как математический с приведённой длиной.
Уравнение колебаний маятника
Колебания математического маятника описываются обыкновенным дифференциальным уравнением вида
где 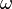
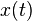
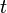
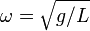
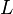
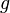
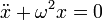
Физический маятник — осциллятор, представляющий собой твёрдое тело, совершающее колебания в поле каких-либо сил относительно точки, не являющейся центром масс этого тела, или неподвижной оси, перпендикулярной направлению действия сил и не проходящей через центр масс этого тела.
Пренебрегая сопротивлением среды, дифференциальное уравнение колебаний физического маятника в поле силы тяжести записывается следующим образом:
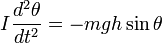
Полагая 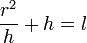
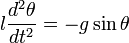
Последнее уравнение аналогично уравнению колебаний математического маятника длиной 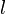
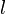
· 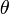
· 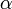
· 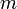
· 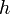
· 
· 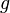
Момент инерции относительно оси, проходящей через точку подвеса:
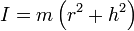
Последнее изменение этой страницы: 2017-03-14; Просмотров: 2137; Нарушение авторского права страницы