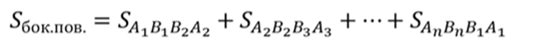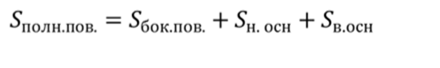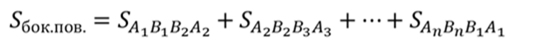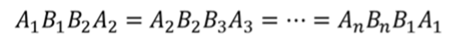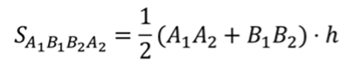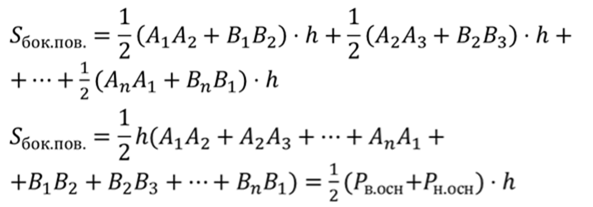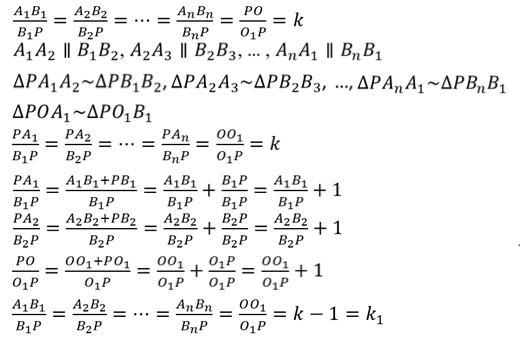какой многогранник называется усеченной пирамидой

Геометрические фигуры. Усеченная пирамида.

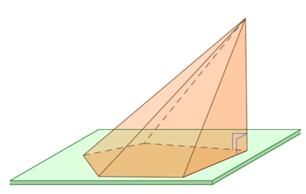
Усеченной пирамидой является многогранник, заключенный меж основанием пирамиды и секущей плоскостью, которая параллельна ее основанию.

Или другими словами: усеченная пирамида — это такой многогранник, который образован пирамидой и ее сечением, параллельным основанию.

Сечение, которое параллельно основанию пирамиды делит пирамиду на 2 части. Часть пирамиды меж ее основанием и сечением — это усеченная пирамида.

Это сечение для усеченной пирамиды оказывается 1-ним из оснований этой пирамиды.

Расстояние меж основаниями усеченной пирамиды является высотой усеченной пирамиды.

Усеченная пирамида будет правильной, когда пирамида, из которой она была получена, тоже была правильной.

Высота трапеции боковой грани правильной усеченной пирамиды является апофемой правильной усеченной пирамиды.

Свойства усеченной пирамиды.

1. Каждая боковая грань правильной усеченной пирамиды является равнобокими трапециями одной величины.

2. Основания усеченной пирамиды являются подобными многоугольниками.

3. Боковые ребра правильной усеченной пирамиды имеют равную величину и один наклонен по отношению к основанию пирамиды.

4. Боковые грани усеченной пирамиды являются трапециями.

5. Двугранные углы при боковых ребрах правильной усеченной пирамиды имеют равную величину.

Формулы для усеченной пирамиды.

Для произвольной пирамиды:

Объем усеченной пирамиды равен 1/3 произведения высоты h (OS) на сумму площадей верхнего основания S₁ (abcde), нижнего основания усеченной пирамиды S₂ (ABCDE) и средней пропорциональной между ними.

h — высота усеченной пирамиды.

Площадь боковой поверхности равняется сумме площадей боковых граней усеченной пирамиды.

Для правильной усеченной пирамиды:

Правильная усеченная пирамида — многогранник, который образован правильной пирамидой и ее сечением, которое параллельно основанию.

Площадь боковой поверхности правильной усеченной пирамиды равна ½ произведения суммы периметров ее оснований и апофемы.

φ — двугранный угол у основания пирамиды.

CH является высотой усеченной пирамиды, P₁ и P₂ — периметрами оснований, S₁ и S₂ — площадями оснований, S_бок — площадью боковой поверхности, S_полн — площадью полной поверхности:

Сечение пирамиды плоскостью, параллельной основанию.

Сечение пирамиды плоскостью, которое параллельно ее основанию (перпендикулярной высоте) разделяет высоту и боковые ребра пирамиды на пропорциональные отрезки.

Сечение пирамиды плоскостью, которое параллельно ее основанию (перпендикулярной высоте) – это многоугольник, который подобен основанию пирамиды, при этом коэффициент подобия этих многоугольников соответствует отношению их расстояний от вершины пирамиды.

Площади сечений, которые параллельны основанию пирамиды, относятся как квадраты их расстояний от вершины пирамиды.

Источник

Что такое усеченная пирамида? Свойства и формулы. Пирамиды индейцев майя

Одним из симметричных полиэдров, свойства которого изучает стереометрия, является пирамида. В данной статье рассмотрим подробнее следующие вопросы: что такое пирамида усеченная, как ее можно получить и какими свойствами она характеризуется.

Полная пирамида

Прежде чем раскрывать вопрос, что такое пирамида усеченная, следует дать определение пирамиды в общем случае.

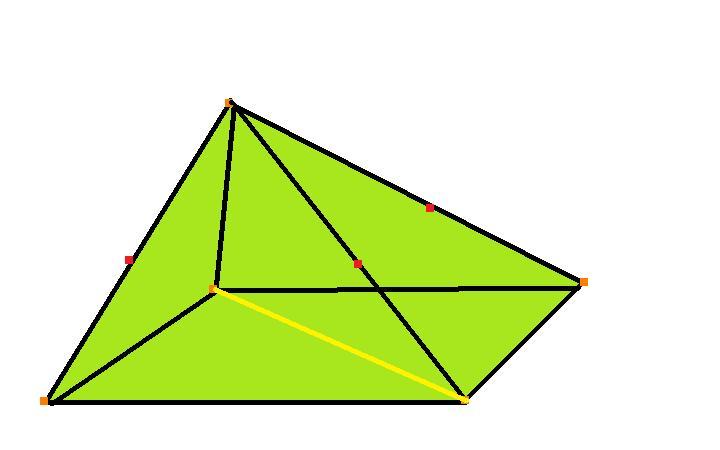
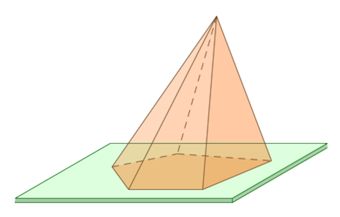
Под пирамидой в геометрии понимают фигуру в трехмерном пространстве, которая состоит из n треугольных граней и одной n-угольной стороны, которая называется основанием. Представить себе пирамиду достаточно просто: необходимо мысленно соединить все углы n-угольника с некоторой одной точкой в пространстве. Рисунок ниже показывает фигуру, которая при этом получается.

Вам будет интересно: Школа №2086: отзывы учеников и родителей, адрес, условия поступления и учебная программа

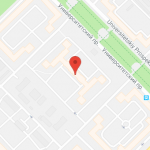
Здесь мы видим, что углы четырехугольного основания соединены отрезками с одной точкой, которая называется вершиной пирамиды. Боковая поверхность фигуры образована четырьмя разными треугольниками.

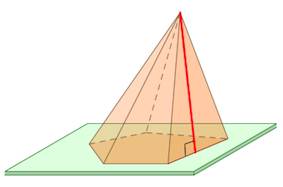
Если все треугольники боковой поверхности будут одинаковыми и равнобедренными, то такая фигура называется прямой пирамидой. Если к тому же основание будет представлять правильный n-угольник, например, квадрат, то говорят о пирамиде правильной.

Усеченная пирамида

Рассмотренная выше фигура называется полной пирамидой. Теперь покажем, что такое усеченная пирамида и как ее можно получить из полной.

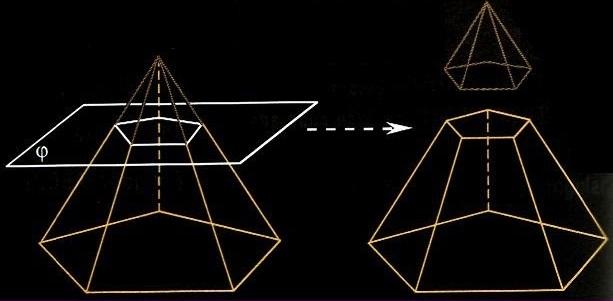
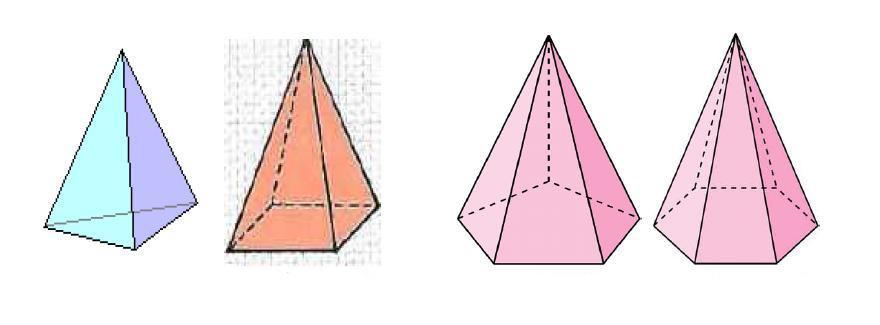
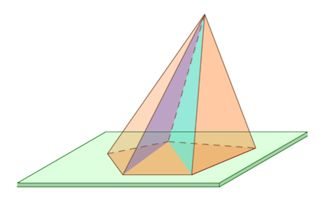
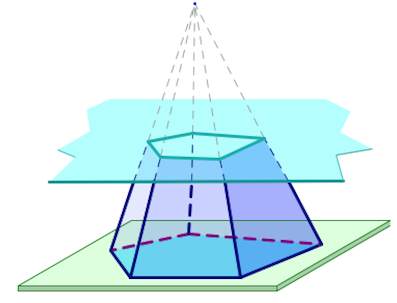
Пусть у нас имеется полная фигура с пятиугольным основанием. Она показана ниже на рисунке слева.

Заметим, что в данном случае мы выбрали секущую плоскость, которая параллельна основанию исходной фигуры. Полученная из правильной фигуры с помощью параллельного сечения усеченная пирамида также будет называться правильной.

Рисунок также показывает, что основания усеченной пирамиды (пятиугольники в примере) образованы подобными правильными многоугольниками, при этом размер верхнего будет всегда меньше, чем нижнего. Боковая поверхность этой фигуры, в отличие от полной пирамиды, образована равнобедренными трапециями.

Если в основании усеченной пирамиды лежит n-угольник, тогда она имеет 2 × n вершин, 3 × n ребер и n + 2 стороны.

Двумя важными геометрическими параметрами рассматриваемой фигуры являются площадь ее поверхности и объем.

Поверхность пирамиды усеченной

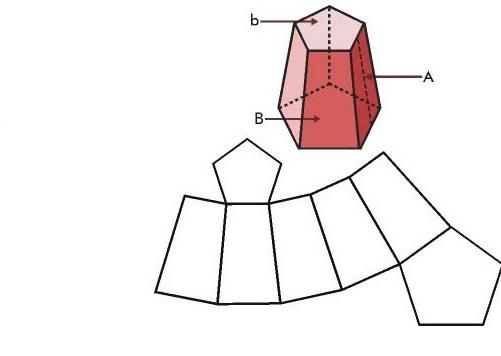
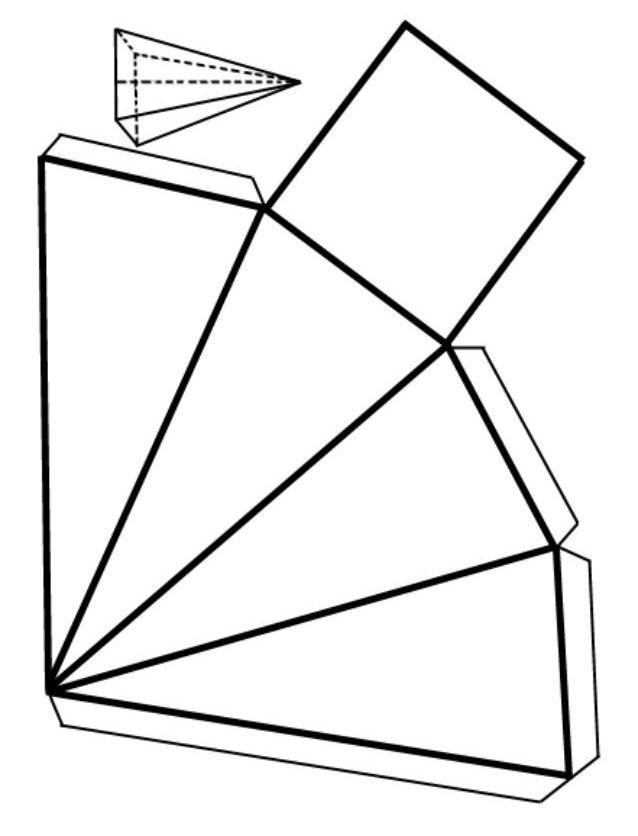
Рассмотрев, что такое усеченная пирамида, перейдем к изучению ее поверхности. Под последней понимают совокупность всех граней, образующих фигуру. Проще всего свойства поверхности изучать на примере развертки. Рисунок ниже показывает развертку для пирамиды с пятиугольными основаниями.

Чтобы вычислить площадь всей ее поверхности, необходимо сложить площадь двух оснований и площадь всех трапеций. Соответствующая формула имеет вид:

S = So1 + So2 + 1/2 × (Po1 + Po2) × Ap.

Например, для случая с четырехугольной правильной усеченной пирамидой эта формула перепишется в виде:

S4 = B2 + b2 + 2 × (B + b ) × Ap.

Объем усеченной пирамиды

Для определения объема рассматриваемой фигуры необходимо знать ее высоту h, а также площади обоих оснований So1 и So2. Если указанные характеристики известны, тогда для определения объема усеченной пирамиды следует воспользоваться формулой:

V = 1/3 × h × (So1 + So2 + √ (So1 × So2)).

Например, для четырехугольной правильной фигуры, длины сторон оснований которой равны B и b, приходим к следующему выражению для объема:

V = 1/3 × h × (B2 + b2 + B × b).

Пример решения задачи

Рассмотрев, что такое усеченная пирамида, а также разобравшись с необходимыми для описания ее характеристик формулами, покажем, как их использовать на практике.

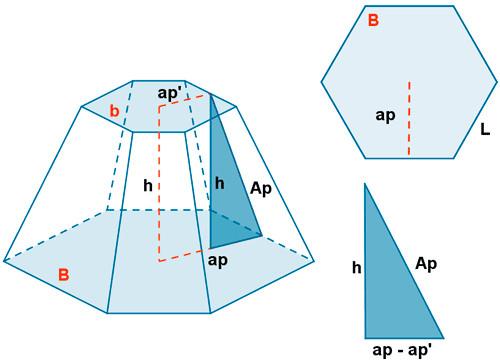
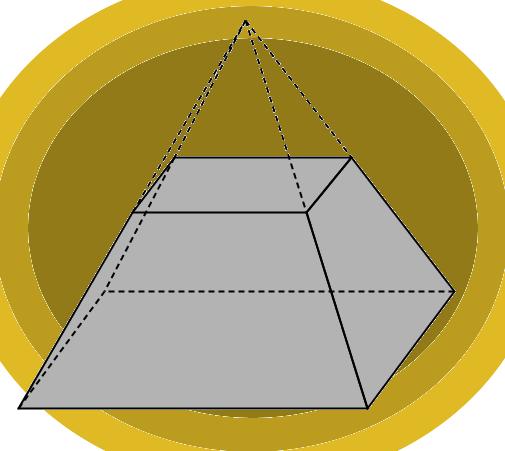
Предположим, что имеется шестиугольная усеченная фигура, которая показана ниже.

Необходимо рассчитать ее объем, если известны стороны оснований B и b и апофема Ap.

Для начала рассчитаем площадь каждого из оснований, которая соответствует площади правильного шестиугольника. Имеем:

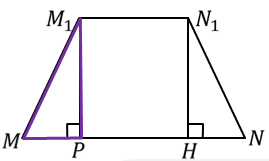
Для определения объема необходимо вычислить через Ap высоту h фигуры. Рассматривая изображенный на рисунке прямоугольный треугольник и применяя теорему Пифагора, получаем:

Тогда объем этой шестиугольной усеченной пирамиды будет равен:

Пирамиды индейцев майя

Если египетские пирамиды с точки зрения геометрии представляют собой правильные полные четырехугольные фигуры, то аналогичные сооружения индейцев майя являются четырехугольными усеченными пирамидами.

Эти памятники культуры, сохранившиеся до наших дней, некогда выполняли двойную роль для своих жителей: с одной стороны, они служили гробницей вождям, с другой же стороны, на их верхнем основании располагался храм, где жрецы поклонялись богам.

Источник

Усеченная пирамида

Урок 28. Геометрия 10 класс ФГОС

В данный момент вы не можете посмотреть или раздать видеоурок ученикам

Чтобы получить доступ к этому и другим видеоурокам комплекта, вам нужно добавить его в личный кабинет, приобрев в каталоге.

Получите невероятные возможности

Конспект урока «Усеченная пирамида»

На прошлых уроках мы работали с пирамидами. Давайте вспомним, какой многогранник называется пирамидой, что такое правильная пирамида, вспомним свойства правильной пирамиды.

Пирамида называется правильной, если ее основание – правильный многоугольник.

Площадь боковой поверхности правильной пирамиды равна половине произведения периметра основания на апофему.

Все боковые ребра правильной пирамиды равны, а боковые грани являются равными равнобедренными треугольниками.

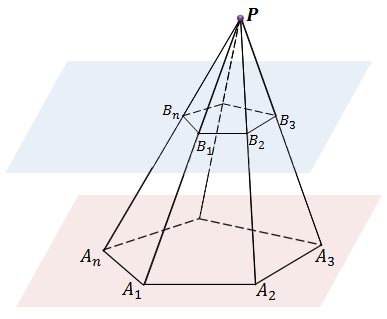
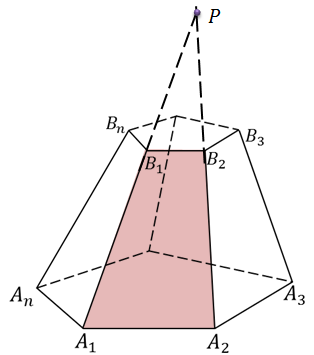
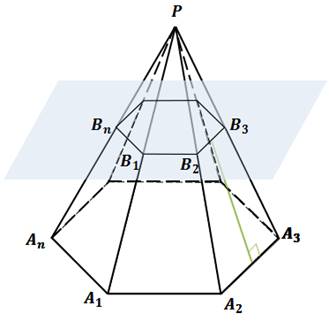
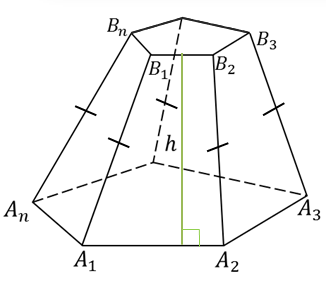
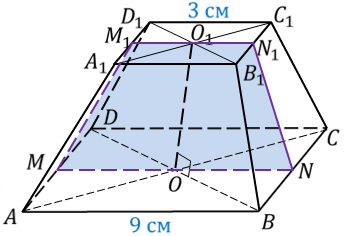
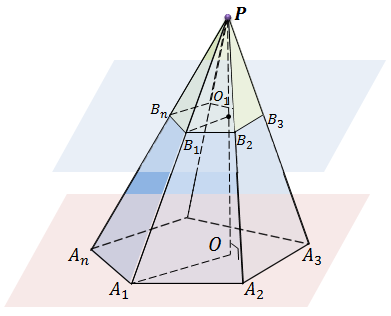
Пусть нам дана пирамида PA₁A₂…A_n. Проведем секущую плоскость β, параллельную плоскости основания пирамиды и пусть эта плоскость пересекает боковые ребра в точках B_1,B₂,…, B_n.

Плоскость β разбивает пирамиду на две фигуры: пирамиду PB₁B₂…B_n и многогранник. Многогранник, гранями которого являются n-угольники A₁A₂…A_n и B₁B₂…B_n, расположенные в параллельных плоскостях и n четырехугольников A₁A₂B₂B₁, A₂A₃B₃B₂,…, A_nA₁B₁B_n называется усеченной пирамидой.

Вокруг нас много примеров усеченных пирамид. Вытяжка над кухонной плитой имеет форму усеченной пирамиды.клавиши клавиатуры и другие предметы.

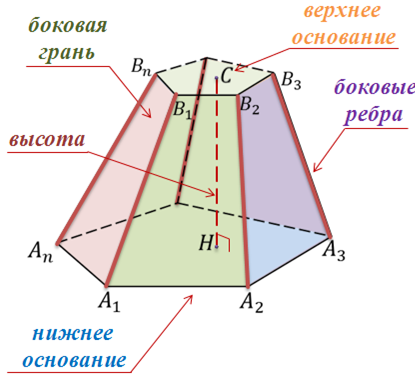
Отрезки A₁B₁,…, A_nB_n называются боковыми рёбрами усеченной пирамиды.

Усеченную пирамиду обозначают так A₁A₂…A_nB₁B₂…B_n. Возьмем на верхнем основании произвольную точку C и из этой точки опустим перпендикуляр на нижнее основание. Этот перпендикуляр называется высотой усеченной пирамиды.

Теперь давайте докажем, что боковые грани усеченной пирамиды – это трапеции.

Для доказательства рассмотрим грань A₁A₂B₂B₁. Понятно, что для других боковых граней доказательство будет проводится аналогично.

Поскольку секущая плоскость проводилась параллельно плоскости основания, то можно записать, что A₁A₂ параллельно B₁B₂. Очевидно, что две другие стороны четырехугольника A₁A₂B₂B₁ не параллельны (они пересекаются в точке P). Получаем, что этот четырехугольник – трапеция. Очевидно, что все остальные боковые грани тоже будут трапециями.

Как и в случае с пирамидой, усеченная пирамида тоже может быть правильной.

Усеченная пирамида называется правильной, если она получена сечением правильной пирамиды плоскостью, параллельной основанию.

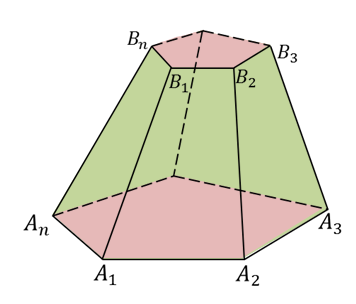
Основаниями усеченной пирамиды являются правильные многоугольники, а боковые грани – равнобедренные трапеции.

Высоты этих трапеций называются апофемами.

Объединение боковых граней называется боковой поверхностью усеченной пирамиды, а объединение всех граней называется полной поверхностью усеченной пирамиды. Тогда площадью боковой поверхности пирамиды называется сумма площадей ее боковых граней.

А площадью полной поверхности пирамиды называется сумма площадей всех ее граней.

Теперь давайте сформулируем и докажем теорему о площади боковой поверхности правильной усеченной пирамиды.

Площадь боковой поверхности правильной усеченной пирамиды равна произведению полусуммы периметров основания на апофему.

Запишем формулу для нахождения площади боковой поверхности усеченной пирамиды.

Поскольку усеченная пирамида правильная, значит, ее гранями будут равнобедренные трапеции.

Площадь равнобедренной трапеции равна произведению полусуммы оснований на высоту. Высота боковой грани есть ничто иное как апофема усеченной пирамиды.

Подставим все в исходную формулу, вынесем половину апофемы за скобки, а в скобках сгруппируем стороны по основаниям. Тогда получим, что площадь боковой поверхности будет равна произведению полусуммы периметров оснований усеченной пирамиды на апофему.

Что и требовалось доказать.

Решим несколько задач.

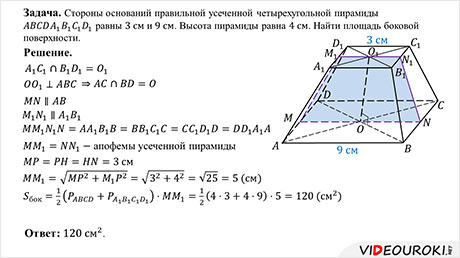
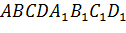
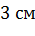
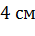
Задача. Стороны оснований правильной усеченной четырехугольной пирамиды равны и . Высота пирамиды равна . Найти площадь боковой поверхности.

Решим еще одну задачу.

Задача. Пирамида пересечена плоскостью, параллельной основанию. Доказать что боковые ребра и высота пирамиды делятся этой плоскостью на пропорциональные части.

Что и требовалось доказать.

Решим еще одну задачу.

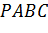
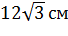
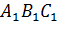
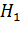
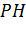
Задача. Правильная треугольная пирамида с высотой и стороной основания равной рассечена плоскостью , проходящей через середину высоты параллельно основанию . Найти площадь боковой поверхности полученной усеченной пирамиды.

Подведем итоги урока. Сегодня на уроке мы познакомились с такими понятиями как усеченная пирамида, правильная усеченная пирамида. Рассмотрели свойства правильной усеченной пирамиды. Решили несколько задач.

Источник

Формулы и свойства правильной четырехугольной пирамиды. Усеченная пирамида

Что такое пирамида в общем случае?

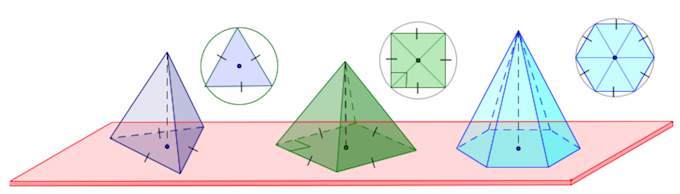
В геометрии под ней понимают объемную фигуру, получить которую можно, если соединить все вершины плоского многоугольника с одной единственной точкой, лежащей в другой плоскости, чем этот многоугольник. Рисунок ниже показывает 4 фигуры, которые удовлетворяют данному определению.

Вам будет интересно: Литовские статуты: даты и история изданий, регламент, хронология принятия статутов

Особым типом пирамид, которые от остальных представительниц класса отличаются идеальной симметрией, являются правильные пирамиды. Чтобы фигура была правильной, должны выполняться следующие два обязательных условия:

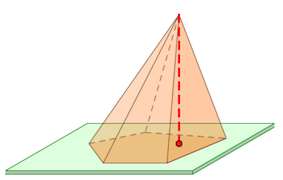
Отметим, что второе обязательное условие можно заменить иным: перпендикуляр, проведенный к основанию из вершины пирамиды (точка пересечения боковых треугольников), должен пересекать это основание в его геометрическом центре.

Правильная четырехугольная пирамида

Теперь перейдем к теме статьи и рассмотрим, какие свойства правильной четырехугольной пирамиды характеризуют ее. Сначала покажем на рисунке, как выглядит эта фигура.

Ее основание является квадратом. Боковые стороны представляют 4 одинаковых равнобедренных треугольника (они также могут быть равносторонними при определенном соотношении длины стороны квадрата и высоты фигуры). Опущенная из вершины пирамиды высота пересечет квадрат в его центре (точка пересечения диагоналей).

Эта пирамида имеет 5 граней (квадрат и четыре треугольника), 5 вершин (четыре из них принадлежат основанию) и 8 ребер. Ось симметрии четвертого порядка, проходящая через высоту пирамиды, переводит ее в саму себя путем поворота на 90o.

Египетские пирамиды в Гизе являются правильными четырехугольными.

Далее приведем формулы, позволяющие определить все характеристики этой фигуры.

Четыре основных линейных параметра

Начнем рассмотрение математических свойств правильной четырехугольной пирамиды с формул высоты, длины стороны основания, бокового ребра и апофемы. Сразу скажем, что все эти величины связаны друг с другом, поэтому достаточно знать только две из них, чтобы однозначно вычислить оставшиеся две.

Предположим, что известна высота h пирамиды и длина a стороны квадратного основания, тогда боковое ребро b будет равно:

Теперь приведем формулу для длины ab апофемы (высота треугольника, опущенная на сторону основания):

Очевидно, что боковое ребро b всегда больше апофемы ab.

Оба выражения можно применять для определения всех четырех линейных характеристик, если известны другие два параметра, например ab и h.

Площадь и объем фигуры

Эту формулу знает каждый школьник. Площадь боковой поверхности, которая образована четырьмя одинаковыми треугольниками, можно определить через апофему ab пирамиды так:

Если ab является неизвестной, то можно ее определить по формулам из предыдущего пункта через высоту h или ребро b.

Общая площадь поверхности рассматриваемой фигуры складывается из площадей So и Sb:

S = So + Sb = a2 + 2 × a × ab = a (a + 2 × ab)

Рассчитанная площадь всех граней пирамиды показана на рисунке ниже в виде ее развертки.

Описание свойств правильной четырехугольной пирамиды не будет полным, если не рассмотреть формулу для определения ее объема. Эта величина для рассматриваемой пирамиды вычисляется следующим образом:

То есть V равен третьей части произведения высоты фигуры на площадь ее основания.

Свойства правильной усеченной четырехугольной пирамиды

Получить эту фигуру можно из исходной пирамиды. Для этого необходимо срезать верхнюю часть пирамиды плоскостью. Оставшаяся под плоскостью среза фигура будет называться пирамидой усеченной.

Боковая поверхность усеченной фигуры образована не треугольниками, а равнобедренными трапециями.

Одним из важных свойств этой пирамиды является ее объем, который рассчитывается по формуле:

V = 1/3 × h × (So1 + So2 + √(So1 × So2))

Источник

Пирамида. Усеченная пирамида

Пирамида – многогранник, основание которого – многоугольник, а остальные грани – треугольники, имеющие общую вершину.

По числу углов основания различают пирамиды треугольные, четырехугольные и т. д.

Вершина пирамиды – точка, соединяющая боковые ребра и не лежащая в плоскости основания.

Основание – многоугольник, которому не принадлежит вершина пирамиды.

Диагональное сечение пирамиды – сечение пирамиды, проходящее через вершину и диагональ основания.

Некоторые свойства пирамиды

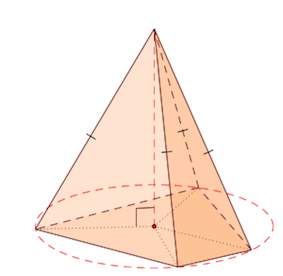
1. Если все боковые ребра равны, то около основания пирамиды можно описать окружность, причем вершина пирамиды проецируется в ее центр.

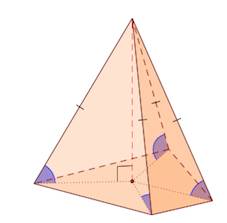
Боковые ребра образуют с плоскостью основания равные углы.

Если боковые ребра образуют с плоскостью основания равные углы, то все боковые ребра пирамиды равны.

Если около основания пирамиды можно описать окружность, причем вершина пирамиды проецируется в ее центр, то все боковые ребра пирамиды равны.

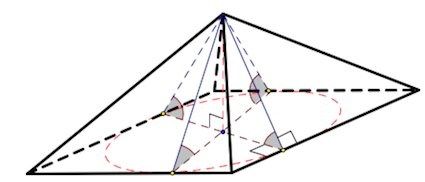
2. Если все грани пирамиды наклонены к плоскости основания под одним углом, то в основание пирамиды можно вписать окружность, причем вершина пирамиды проецируется в ее центр.

Виды пирамид

Пирамида называется правильной, если основанием ее является правильный многоугольник, а вершина проецируется в центр основания.

Для правильной пирамиды справедливо:

Пирамида называется прямоугольной, если одно из боковых ребер пирамиды перпендикулярно основанию. Тогда это ребро и есть высота пирамиды.

Усеченной пирамидой называется многогранник, заключенный между основанием пирамиды и секущей плоскостью, параллельной ее основанию.

Усеченная пирамида является правильной, если она представляет собой часть правильной пирамиды.

Свойства усеченной пирамиды:

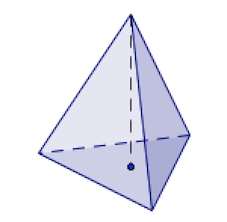
Тетраэдр – треугольная пирамида. В тетраэдре любая из граней может быть принята за основание пирамиды.

В правильном тетраэдре все четыре грани являются равносторонними треугольниками.

От тре­уголь­ной пи­ра­ми­ды, объем ко­то­рой равен 12, от­се­че­на тре­уголь­ная пи­ра­ми­да плос­ко­стью, про­хо­дя­щей через вер­ши­ну пи­ра­ми­ды и сред­нюю линию ос­но­ва­ния. Най­ди­те объем от­се­чен­ной тре­уголь­ной пи­ра­ми­ды.

В основании пирамиды лежит прямоугольный треугольник, один из катетов которого равен 8 см, а радиус описанной около него окружности равен 5 см. Высота пирамиды равна 12 см. Вычислите боковые ребра пирамиды.

Высота правильной четырехугольной пирамиды равна 4. Боковое ребро наклонено к плоскости основания под углом 30°. Найдите боковое ребро пирамиды. Укажите промежутки, которым принадлежит числовое значение ребра.

Источник