какой многофазный приемник является симметричным
ЛЕКЦИЯ 8. Трехфазный приемник, соединенный по схеме «звезда»



Трехфазный приемник, соединенный по схеме «звезда»
Симметричный трехфазный приемник – это приемник, у которого комплексные сопротивления фаз равны между собой 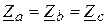
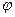
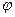
Трехфазный приемник, соединенный по схеме «звезда»
Из формулы следует, что при равенстве комплексных проводимостей фаз междуузловое напряжение будет равно 0, так как
Согласно II ЗК для контуров трехфазной системы:
Следовательно, напряжения фаз приемника:
Так как UnN = 0, то для симметричного приемника фазные напряжения приемника равны фазным напряжениям генератора:
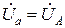
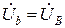
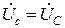
Определив фазные напряжения, находят фазные токи:
İа = 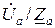
İb = 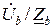
İс = 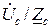
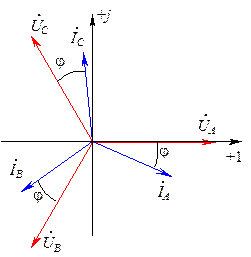
Для построения векторной диаграммы достаточно задаться начальной фазой одного из напряжений цепи, например jAB= + 30°.
На комплексной плоскости строятся в масштабе векторы фазных напряжений 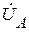
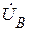
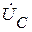
|
Векторная диаграмма симметричного приемника
Симметричный трехфазный приемник подключают к трехпроводной системе.
Несимметричный трехфазный приемник. Это приемник, у которого комплексные сопротивления фаз не равны между собой:
Схема несимметричного приемника.
Как видно из приведенного, у такого приемника могут быть не равны между собой модули фаз, аргументы равны; равны между собой модули фаз, аргументы фаз не равны; не равны между собой как модули так и аргументы фаз. В этом случае напряжение между нейтральной точкой генератора и нейтральной точкой приемника не будет равно нулю.
Фазные напряжения и токи приемника определяются по формулам
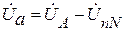
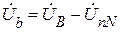
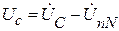
где 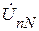
где для приведенной схемы:
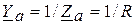
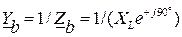
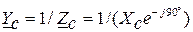
По закону Ома определяются фазные токи:
При построении векторной диаграммы необходимо сначала построить векторы напряжений источника 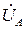
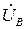
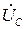
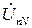
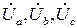
Векторная диаграмма напряжений и токов при смещении нейтрали
Из векторной диаграммы следует, что асимметрия нагрузки в трехпроводной сети приводит к перекосу фазных напряжений, что недопустимо. Поэтому трехпроводная система при несимметричной нагрузке и схеме «звезда» не применяется.
Из приведенных формул видно, что фазные напряжения приемника будут отличаться как от фазных напряжений генератора, так и относительно друг друга. В этом случае наступает «перекос» фазных напряжений приемника, что приводит к перенапряжению фаз приемника, токи фаз превышают номинальные значения, что является недопустимым.
В этом случае нарушается симметрия фазных напряжений на приемнике:
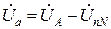
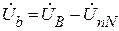
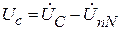
где 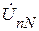
Анализ формул показывает, что для выравнивания фазных напряжений приемника необходимо получить значение напряжения между нейтральными точками генератора и приемника равное 0. Это возможно при равенстве знаменателя бесконечности, т. е., если принять ZnN = 0, то YnN = ¥. На практике это достигается включением провода, сопротивление которого мало, между нейтралями генератора и приемника. Тогда
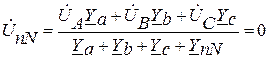
В этом случае напряжения на фазах приемника остаются практически симметричными, равными напряжению генератора.
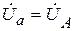
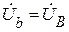
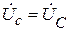
Для нижеприведенной схемы значения комплексных полных проводимостей:
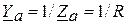
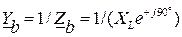
Схема несимметричного приемника,
включенного в четырех проводную систему
По закону Ома определяются фазные токи:
Ток нулевого провода
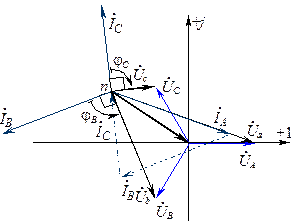
Векторная диаграмма несимметричного трехфазного приемника, включенного в четырехпроводную систему
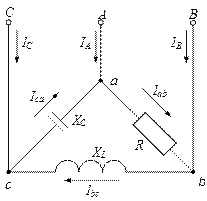
Соединение фаз приемника по схеме «треугольник»
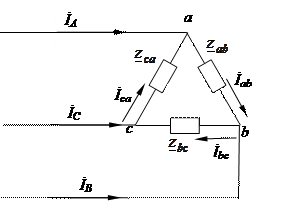 |
Схема трехфазного приемника, соединенного по схеме треугольник
По фазам приемника протекают фазные токи İав, İвс, İса. Условное положительное направление фазных токов приемника от начала к концу фаз. Условные положительные направления фазных напряжений совпадают с положительным направлением фазных токов. Условное положительное направление линейных токов İА, İВ, İС принято от генератора к приемнику.
Напряжение между началом и концом фазы при соединении треугольником – это напряжение между линейными проводами. Поэтому при соединении треугольником линейное напряжение равно фазному напряжению:
При подключении приемника, соединенного треугольником, к источнику питания по фазам приемника протекает фазный ток, который определяется по закону Ома:
Линейные токи можно определить из уравнений, составленных по II ЗК для точек а, в, с соответственно:
Таким образом, получаем
İА=İав – İса;
Итак,линейные токи при соединении треугольником равны векторной разности фазных токов тех фаз, которые соединены с данным линейным проводом.
Как следует из вышеприведенных уравнений, векторная сумма линейных токов всегда равна нулю:
Система линейных (фазных) токов при соединении треугольником образует такой же замкнутый треугольник, как система линейных (фазных) напряжений и при соединении звездой. Фазные токи при симметричной нагрузке равны по значению и сдвинуты по отношению к векторам напряжений на одинаковый угол φ.
Для определения линейных токов строем векторную диаграмму фазных токов. Так как линейные токи определяются через фазные так же, как и линейные напряжения через фазные при соединении звездой, то можно сразу построить векторы линейных токов, соединив концы векторов фазных токов.
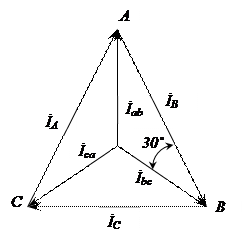 |
. Векторная диаграмма фазных и линейных токов при соединении фаз треугольником
Векторы линейных токов образуют замкнутый треугольник. Поскольку при симметричной нагрузке системы фазных и линейных токов симметричны, сравнивая векторные диаграммы токов схемы треугольник и напряжений схемы звезда, можно заключить, что линейные токи при симметричной нагрузке, соединенной треугольником, в 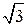
Iл = 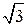
Несимметричная нагрузка при соединении треугольником. Трехпроводная система. При соединении треугольником Uл = Uф, а линейные напряжения источника всегда симметричны. Поэтому соединение треугольником применяется в трехпроводных системах при любой нагрузке, как симметричной, так и несимметричной, если номинальное напряжение приемника равняется линейному напряжению источника питания.
|
.Схема несимметричного приемника, соединенного по схеме треугольник
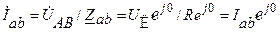
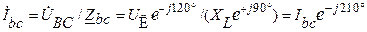
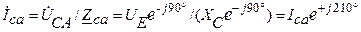
Линейные токи определяются по II ЗК для узлов a, b, c:
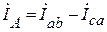
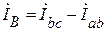
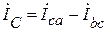
Для построение векторной диаграммы на комплексной плоскости сначала строятся векторы линейных напряжений, затем векторы фазных токов и по ним определяются графически линейные токи, которые должны совпасть с расчетными по модулю и аргументу.
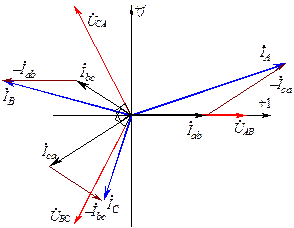
Векторная диаграмма напряжений, фазных и линейных токов при
соединении фаз приемника треугольником при несимметричной нагрузке
Расчет трехфазных цепей
Трехфазные цепи являются разновидностью цепей синусоидального тока, и, следовательно, все рассмотренные ранее методы расчета и анализа в символической форме в полной мере распространяются на них. Анализ трехфазных систем удобно осуществлять с использованием векторных диаграмм, позволяющих достаточно просто определять фазовые сдвиги между переменными. Однако определенная специфика многофазных цепей вносит характерные особенности в их расчет, что, в первую очередь, касается анализа их работы в симметричных режимах.
Расчет симметричных режимов работы трехфазных систем
Многофазный приемник и вообще многофазная цепь называются симметричными, если в них комплексные сопротивления соответствующих фаз одинаковы, т.е. если 

Если к симметричной трехфазной цепи приложена симметричная трехфазная система напряжений генератора, то в ней будет иметь место симметричная система токов. Такой режим работы трехфазной цепи называется симметричным. В этом режиме токи и напряжения соответствующих фаз равны по модулю и сдвинуты по фазе друг по отношению к другу на угол 

Так для симметричного режима работы цепи на рис. 2,а при известных линейном напряжении и сопротивлениях фаз 

где 

Тогда на основании вышесказанного


Комплексы линейных токов можно найти с использованием векторной диаграммы на рис. 2,б, из которой вытекает:
При анализе сложных схем, работающих в симметричном режиме, расчет осуществляется с помощью двух основных приемов:
Все треугольники заменяются эквивалентными звездами. Поскольку треугольники симметричны, то в соответствии с формулами преобразования «треугольник-звезда» 
Так как все исходные и вновь полученные звезды нагрузки симметричны, то потенциалы их нейтральных точек одинаковы. Следовательно, без изменения режима работы цепи их можно (мысленно) соединить нейтральным проводом. После этого из схемы выделяется базовая фаза (обычно фаза А), для которой и осуществляется расчет, по результатам которого определяются соответствующие величины в других фазах.
Пусть, например, при заданном фазном напряжении 


В соответствии с указанной методикой выделим расчетную фазу А, которая представлена на рис. 4. Здесь 

Тогда для тока 

и соответственно 
Расчет несимметричных режимов работы трехфазных систем
Если хотя бы одно из условий симметрии не выполняется, в трехфазной цепи имеет место несимметричный режим работы. Такие режимы при наличии в цепи только статической нагрузки и пренебрежении падением напряжения в генераторе рассчитываются для всей цепи в целом любым из рассмотренных ранее методов расчета. При этом фазные напряжения генератора заменяются соответствующими источниками ЭДС. Можно отметить, что, поскольку в многофазных цепях, помимо токов, обычно представляют интерес также потенциалы узлов, чаще других для расчета сложных схем применяется метод узловых потенциалов. Для анализа несимметричных режимов работы трехфазных цепей с электрическими машинами в основном применяется метод симметричных составляющих, который будет рассмотрен далее.
При заданных линейных напряжениях наиболее просто рассчитываются трехфазные цепи при соединении в треугольник. Пусть в схеме на рис. 2,а 



По найденным фазным токам приемника на основании первого закона Кирхгофа определяются линейные токи:


Искомые углы a и b могут быть также найдены аналитически на основании теоремы косинусов:
При соединении фаз генератора и нагрузки в звезду и наличии нейтрального провода с нулевым сопротивлением фазные напряжения нагрузки равны соответствующим напряжениям на фазах источника. В этом случае фазные токи легко определяются по закону Ома, т.е. путем деления известных напряжений на фазах потребителя на соответствующие сопротивления. Однако, если сопротивление нейтрального провода велико или он отсутствует, требуется более сложный расчет.
Рассмотрим трехфазную цепь на рис. 6,а. При симметричном питании и несимметричной нагрузке 

Разность потенциалов нейтральных точек генератора и нагрузки называется напряжением смещения нейтральной точки (обычно принимается, что 
Для расчета токов в цепи на рис. 6,а необходимо знать напряжение смещения нейтрали. Если оно известно, то напряжения на фазах нагрузки равны:

Тогда для искомых токов можно записать:

Соотношение для напряжения смещения нейтрали, записанное на основании метода узловых потенциалов, имеет вид
 . . | (1) |
При наличии нейтрального провода с нулевым сопротивлением 







Запишем выражения комплексных сопротивлений фаз нагрузки:
Тогда для напряжения смещения нейтрали будем иметь
Напряжения на фазах нагрузки (здесь и далее индекс N у фазных напряжений источника опускается)
Таким образом, наиболее ярко будет гореть лампочка в фазе С.
В заключение отметим, что если при соединении в звезду задаются линейные напряжения (что обычно имеет место на практике), то с учетом того, что сумма последних равна нулю, их можно однозначно задать с помощью двух источников ЭДС, например, 


 . . | (2) |
Контрольные вопросы и задачи
200 тыс км/с в стекле и




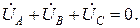
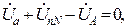
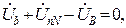
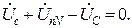
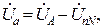
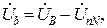
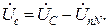

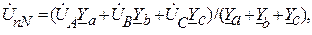
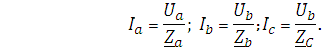
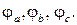
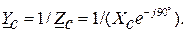
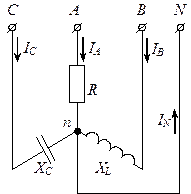
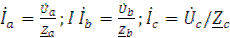

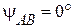 . Тогда
. Тогда 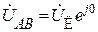 ;
; 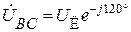 ;
; 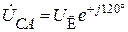 . Комплексные сопротивления приемника
. Комплексные сопротивления приемника 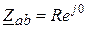 ;
; 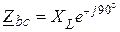 ;
; 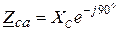 .
.