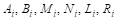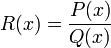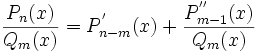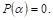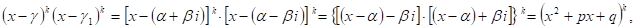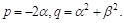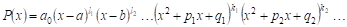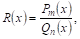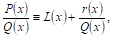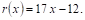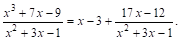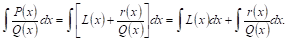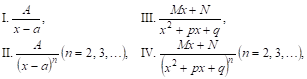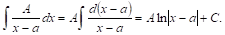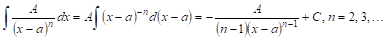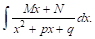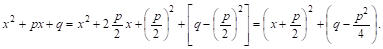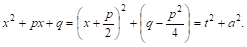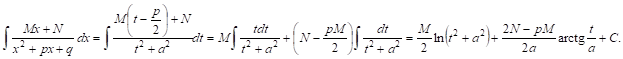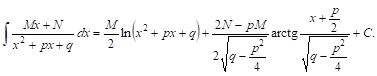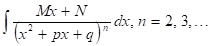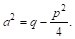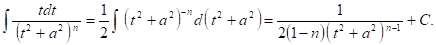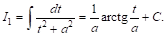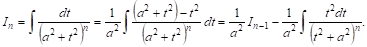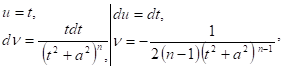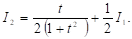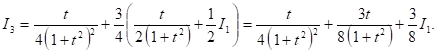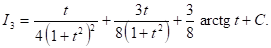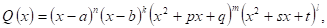какой многочлен не может быть знаменателем рациональной дроби

Рациональная дробь

Рациональная дробь

Рациональная дробь — это дробь, числителем и знаменателем которой являются многочлены. Она имеет вид

где P(x) и Q(x) некоторые многочлены.

Различают правильные и неправильные рациональные дроби, по аналогии с обычными числовыми дробями. Рациональная дробь называется правильной, если порядок знаменателя больше порядка числителя, и неправильной, если наоборот.

Любую неправильную рациональную дробь можно преобразовать в сумму некоторого многочлена и правильной рациональной дроби

Любую рациональную дробь многочленов с вещественными коэффициентами можно представить как сумму рациональных дробей, знаменателями которых являются выражения (x − a) k (a — вещественный корень Q(x)) либо (x 2 + px + q) k (где x 2 + px + q не имеет действительных корней), причём степени k не больше кратности соответствующих корней в многочлене Q(x). На основании этого утверждения основана теорема об интегрируемости рациональной дроби. Согласно ей, любая рациональная дробь может быть интегрирована в элементарных функциях, что делает класс рациональных дробей весьма важным в математическом анализе.

См. также

Полезное

Смотреть что такое «Рациональная дробь» в других словарях:

Дробь (математика) — У этого термина существуют и другие значения, см. Дробь. 8 / 13 числитель числитель знаменатель знаменатель Две записи одной дроби Дробь в математике число, состоящее из одной или нескольких частей… … Википедия

Дробь — В Викисловаре есть статья «дробь» Наименование символа «⁄» (другое, распространённое по большей части в английском языке, название символа солидус (англ.), или слэш), например, в номерах домов. Так номер дома «5/17» читается «пять… … Википедия

РАЦИОНАЛЬНАЯ ФУНКЦИЯ — 1) Р. ф. функция w=R(z), где R(z) рациональное выражение от z, т. е. выражение, полученное из независимого переменного z и нек рого конечного набора чисел (действительных или комплексных) посредством конечного числа арифметич. действий. Р. ф.… … Математическая энциклопедия

РАЦИОНАЛЬНОЕ ЧИСЛО — число, выражаемое рациональной дробью. Формальная теория Р. ч. строится с помощью пар целых чисел. Р а ц и о н а л ь н о й д р о б ь ю наз. упорядоченная пара ( а, b )целых чисел а и b, у к рой b№0. Две рациональные дроби и наз. э к в и в а л е н … Математическая энциклопедия

Источник

Дробно-рациональные уравнения

Что такое дробно-рациональные уравнения

Дробно-рациональными уравнениями называют такие выражения, которые представляется возможным записать, как:

при P ( x ) и Q ( x ) в виде выражений, содержащих переменную.

Таким образом, дробно-рациональные уравнения обязательно содержат как минимум одну дробь с переменной в знаменателе с любым модулем.

1 2 x + x x + 1 = 1 2

Уравнения, которые не являются дробно-рациональными:

Как решаются дробно-рациональные уравнения

В процессе решения дробно-рациональных уравнений обязательным действием является определение области допустимых значений. Найденные корни следует проверить на допустимость, чтобы исключить посторонние решения.

Алгоритм действий при стандартном способе решения:

Разберем предложенный алгоритм на практическом примере. Предположим, что имеется дробно-рациональное уравнение, которое требуется решить:

Начать следует с области допустимых значений:

Воспользуемся правилом сокращенного умножения:

В результате общим знаменателем дробей является:

Выполним умножение каждого из членов выражения на общий знаменатель:

После сокращения избавимся от скобок и приведем подобные слагаемые:

Осталось решить квадратное уравнение:

Согласно ОДЗ, первый корень является лишним, так как не удовлетворяет условию, по которому корень не равен 2. Тогда в ответе можно записать:

Примеры задач с ответами для 9 класса

Требуется решить дробно-рациональное уравнение:

Определим область допустимых значений:

Квадратный трехчлен x 2 + 7 x + 10 следует разложить на множители, руководствуясь формулой:

Сократим дроби, избавимся от скобок, приведем подобные слагаемые:

Потребуется решить квадратное уравнение:

Первый корень не удовлетворяет условиям ОДЗ, поэтому в ответ нужно записать только второй корень.

Дано дробно-рациональное уравнение, корни которого требуется найти:

В первую очередь следует переместить все слагаемые влево и привести дроби к минимальному единому знаменателю:

Заметим, что получилось нулевое значение для дроби. Известно, что дробь может равняться нулю, если в числителе нуль, а знаменатель не равен нулю. На основании этого можно составить систему:

Следует определить такие значения для переменной, при которых в дроби знаменатель будет обращаться в нуль. Такие значения необходимо удалить из ОДЗ:

Далее можно определить значения для переменных, которые при подстановке в уравнение обращают числитель в нуль:

Получилось квадратное уравнение, которое можно решить:

Сравнив корни с условиями области допустимых значений, можно сделать вывод, что оба корня являются решениями данного уравнения.

Нужно решить дробно-рациональное уравнение:

На первом шаге следует перенести все слагаемые в одну сторону и привести дроби к минимальному единому знаменателю:

Перечисленные значения переменной обращают знаменатель в нуль. По этой причине их необходимо удалить из области допустимых значений.

Корни квадратного уравнения:

Заметим, что второй корень не соответствует ОДЗ. Таким образом, в ответе остается только первый корень.

Найти корни уравнения:

Согласно стандартному алгоритму решения дробно-рациональных уравнений, выполним перенос всех слагаемых в одну сторону. Далее необходимо привести к дроби к наименьшему общему знаменателю:

Такое значение переменной, при котором знаменатель становится равным нулю, нужно исключить из области допустимых значений:

Заметим, что это частный случай линейного уравнения, которое обладает бесконечным множеством корней. При подстановке какого-либо числа на место переменной х в любом случае числовое равенство будет справедливым. Единственным недопустимым значением для х в данном задании является число 3, которое не входит в ОДЗ.

Ответ: х — любое число, за исключением 3.

Требуется вычислить корни дробно-рационального уравнения:

На первом этапе необходимо выполнить перенос всех слагаемых влево, привести дроби к минимальному единому знаменателю:

Данные значения переменной х являются недопустимыми, так как в этом случае теряется смысл дроби в связи с тем, что знаменатель принимает нулевое значение.

Заметим, что 2 не входит в область допустимых значений. В связи с этим, можно заключить, что у уравнения отсутствуют корни.

Ответ: корни отсутствуют

Нужно найти корни уравнения:

Начнем с определения ОДЗ:

При умножении обеих частей уравнения на единый знаменатель всех дробей и сокращении аналогичных выражений, которые записаны в числителе и знаменателе, получим:

Прибегая к арифметическим преобразованиям, можно записать уравнение в упрощенной форме:

Второе значение не соответствует области допустимых значений.

Источник

17. Многочлен. Рациональные дроби. Интегрирование простейших рациональных дробей

Как известно, Многочленом или Целой рациональной функцией называется функция вида

(6)

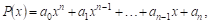
Где П — Целое положительное число, называемое СтЕПенью многочлена, а 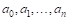— постоянные Числа — Коэффициенты Многочлена.

Корнем многочлена Р(Х) называется всякое число A (действиТельное, мнимое или комплексное), обращающее многочлен в нуль, т. е. такое, что

Напомним ряд теорем, используемых в дальнейшем изложении.

Теорема 1. Всякий многочлЕН имеет по крайнеЙ мере один действительный или комплексный корень.

Далее имеет место теорема Безу:

(7)

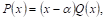
Где Q(X) — многочлен, степень которого на единицу меньше степени многочлена Р(х).

Замечание. Очевидно, коэффициент при старшей степени Х В многочлене Q(X) равен коэффициенту при старШЕй степени Х в многочлене Р(Х).

Теорема 3. Всякий многочлен степени П может быть представлен В виде произведения п линейных множителей вида 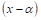и постоянного числа A0 — коэффициента при старшей степени х.

Следствие. Многочлен Р(Х) степени п имеет не более Чем п различных корней.

Теорема 4. Если многочлен тождественно равен нулю, то все его коэффициенты равны нулю.

Следствие. Если два многочлена тождественно равны друг другу, то коэффициенты при одинаковых степенях равны между собой.

Пусть Р(Х) — многочлен степени П. По теореме 3 его можно представить в видЕ произведения П линейных множителей

(8)

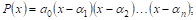
Среди линейных множИТелей, на которые разложен многочлен, могут быть одинаковые. Объединяя в разложении (8) одинаковые сомножители, мы можем его записать в виде

Корень А многочлена Р(Х), для которого линейный множитель в разложении (8) встречается Т раз, называется Корнем кратности т. Корень кратности единица называется Простым.

Теперь, когда введено понятие о кратности корня, мы можем уточнить теорему о числе корней многочлена (см. следствие к теореме 3).

Теорема 5. Всякий многочлен П-й степени имеет ровно П Корней, если каждый корень считать столько раз, какова его кратность.

Доказательство этой теоремы непосредственно вытекает из формулы разложения многочлена на линейные множители.

Среди корней многочлена могут быть и Комплексные. Для них имеет место следующая теорема.

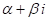
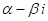
Теорема 6. Если многочлен с действительными КоэффиЦиентами имеет комплексный корень , То Сопряженное число также является корнем многочлена.

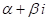
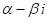
ТЕОрема 7. Если многочлен с действительными КоэффиЦиентами имеет корнем комплексное число Кратности K, то сопряженное число Также является корнем многочлена той же кратности.

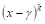
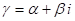
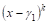
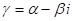
Из этой теоремы непосредственно следует: если в разложении многочлена на множители имеется множитель , соответствующий комплексному корню , то в этом разложении имеется множитель , соответствующий сопряженному корню . Перемножая попарно множители, соответствуюЩие сопряженным корням, получим

Где

Это позволяЕТ заменить произведение линейных множителей, соответствующих Сопряженным корням, квадратным трехчленом с действительными коэффициентами.

Все вышЕИзложенное позволяет высказать следующее окончательное предложение, с помощью которого удается избежать мнимых чисел при разложении многочлена на множители.

Всякий многочлен с действительными коэффициентами можно прЕДставить в следующей форме:

В этом разложении Линейные множители соответствуют действительным корням многочлена, а квадратные трехчлены, соответствуют комплексным корням многочлена.

Постоянные 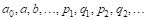являются действительными числами.

Дробной рациональной функцией или просто рациональной дробью называется функция, равная частному от деления двух многочленов:

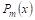
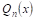
Где — многочлен степени Т, a — Многочлен СТепени N.

Например, 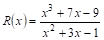является рациональной дробью.

Рациональная дробь называется Правильной, если степень числителя меньше степени знаменателя, и Неправильной — В противном случае. Приведенная выше рациональная дробь неправильна.

Многочлен, очевидно, является частным случаем рациональной дроби, знаменатель которой есть многочлен нулевой степени (постоянное число).

Задача настоящей главы заключается в изложении методов интегрирования рациональных дробей, отличных от многочленов. Что касается многочленов, то мы уже знаем, что они легко интегрируются.

Переходя к интегрированию рациональных дробей, отметим, прежде всего, что Всякую неправильную рациональную дробь можно представить в ВИде суммы многочлена и правильной рациональной дроби.

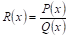
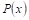
В самом деле, пусть — Неправильная рациональная дробь, т. Е. степень больше или равна степени Q(Х). Разделив числитель на знаменатель, получим тождество

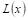
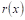
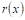
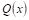
Где и — многочлены, причем степень остатков меньше степени знаменателя дроби .

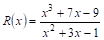
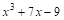
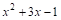
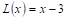
Например, пусть . Разделив на , получим частное и остаток

Следовательно,

Это замечание показывает, что интегрированиЕ неправильной рациональной дроби сводится к интегрированию многочлена и правильной рациональной дроби :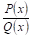

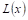
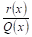
Так как многочлены мы интегрировать умеем, то задача сводится к интегрированию правильных рациональных дробей.

Как будет показано ниже всякую правильную рациональную дробЬ можно представить в виде суммы конечного числа так называемых Простейших дробей следующих четырех типов:

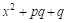
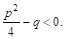
Где А, а, Р, Q, М, N — действительные числа, а трехчлен Не имеет действительных корней, т. е. Поэтому, EcЛи мы научимся интегрировать простейшие ДРоби и разлагать правильную рациональную дробь на сумму простейших, то задача интегрирования рациональных функций будет решена.

Интегрирование простейших дробей I и II типов не представляет никакого труда. В самом деле:

Перейдем теперь к интегрированию рациональных дробей III и IV типов.

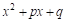
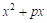
Рассмотрим отдельно знаменатель и Дополним до полного квадрата:

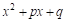
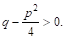
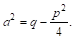
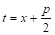
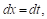
Так как по условию трехчлен не имеет действительных корней, то Положим для простоты Применим теперь к интегралу замену переменного, положив тогда

Заменяя, наконец, T И А их выражениями, получим

Введем новую переменную T, положив ее равной половине производной знаменателя:

Тогда

Рассмотрим интегрирование дробей IV типа:

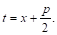
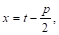
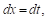
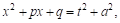
Введем, как и в случае III, новую переменную T, положив Это дает где, как и выше,

Следовательно, 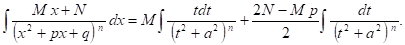(10)

Первый из этих интегралов Соотношения (10) легко вычисляется:

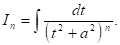
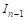
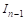
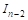
Итак, остается вычислить интеграл Мы здесь предложим способ вычисления этого интеграла с помощью рекуррентной формулы. Мы будем выражать последовательно через , через и т. Д., пока не дойдем до

К интегралу 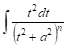применим метод интегрирования по частям, полагая

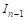
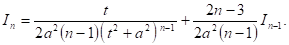
И группируя члены, содержащие , получим

(11)

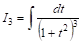
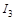
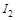
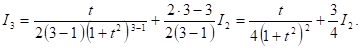
Это и есть искомая рекуррентная формула. Покажем способ ее применения. Пусть требуется вычислить . Применяя рекуррентную формулу (11), выразим через :

(12)

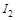
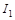
Применяя ту же рекуррентную формулу для N = 2, выразим через :

Подставляя выражение 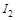в (12), найдем

Так как 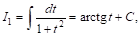то окончательно

Таким образом, чтобы закончить вопрос об интегрировании рациональных дробей, нам остается Показать, как всякую Правильную раЦиональную дробь можно рАЗложить На сумму Простейших.

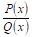
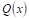
Искомая формула разложения правильной рациональной дроби на простейшие состоит в следующем. Пусть знаменатель дроби имеет вид:

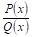
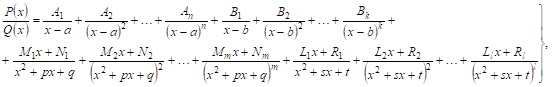
Причем квадратные трехчлены в этом выражении не имеют действительных корней, тогда правильную дробь можно представить в виде следующей сумы простейших дробей:

(13)

Где 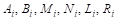— действительные числа. (Примем без доказательства).

Из формулы (13) мы видим, что линейным множителям Знаменателя 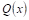соответствуют простейшие дроби I и II типа, а квадратным множителям соответствуют простейшие дроби III и IV типа.

При этом число простейших дробей, соответствующих данному множителю (линейному или квадратному), равно степени, с которой этот множитель входит в разложение знаменателя ДроБи на множители.

Для того чтобы можно было пользоваться формулой (13), Надо научиться определять коэффициенты . Этому посвящен следующий подраздел.

Источник