какой метод сортировки самый быстрый
О сортировках (пузырьковой, быстрой, расческой. )
Эта статья ориентирована в первую очередь на начинающих программистов. О сортировках вообще и об упомянутых в заголовке в интернете море статей, зачем нужно еще одна? Например, есть хорошая статья здесь, на хабре: Пузырьковая сортировка и все-все-все. Во-первых, хорошего много не бывает, во-вторых в этой статье я хочу ответь на вопросы «зачем, что, как, почему».Зачем нужны сортировки? В первую очередь, для поиска и представления данных. Некоторые задачи с неотсортированными данными решить очень трудно, а некоторые просто невозможно. Пример: орфографический словарь, в нем слова отсортированы по алфавиту. Если бы это было не так, то попробуйте найти в нем нужное слово. Телефонная книга, где абоненты отсортированы по алфавиту. Даже если сортировка не обязательна и не сильно нужна, все равно бывает удобнее работать с отсортированными данными.
Время сортировки 100001 элемента
Измерим время сортировки для массива, содержащего 100001 элемент на компьютере с процессором Intel i5 (3.3Ггц).Время указано в сек, через дробь указано количество проходов (для быстрой сортировки оно неизвестно).Как и ожидалось, шейкерная сортировка на проблемном массиве (который полностью упорядочен, только первый и последний элементы переставлены) абсолютный лидер. Она идеально «заточена» под эти данные. Но на случайных данных сортировки расческой и qsort не оставляют соперницам шанса. Пузырьковая сортировка на проблемном массиве показывает двукратное увеличение скорости по сравнению с случайным просто потому, что количество операций перестановки на порядки меньше.
| Сортировка | Простая | Пузырьковая | Шейкерная | Расчёской | Быстрая (qsort) |
|---|---|---|---|---|---|
| Стабильная | + | + | + | — | — |
| Случайный | 23.1/100000 | 29.1/99585 | 19.8/50074 | 0.020/49 | 0.055 |
| Проблемный | 11.5/100000 | 12.9/100000 | 0.002/3 | 0.015/48 | 0.035 |
| Обратный | 18.3/100000 | 21.1/100000 | 21.1/100001 | 0.026/48 | 0.037 |
А теперь вернемся к истокам, к пузырьковой сортировке и воочию посмотрим на процесс сортировки. Видите, как на первом проходе тяжелый элемент (50) переносится в конец?

Сравниваемые элементы показаны в зеленых рамках, а переставленные — в красных
Дополнение после публикации
Я ни коей мере не считаю qsort плохой или медленной — она достаточно быстра, функциональна и при возможности следует пользоваться именно ею. Да, ей приходится тратить время на вызов функции сравнения и она уступила «расческе», которая сравнивает «по месту». Это отставание несущественно (сравните с отставанием пузырька от qsort, которое будет увеличиваться при росте массива). Пусть теперь надо сравнивать не числа, а какую-то сложную структуру по определенному полю и пусть эта структура состоит из 1000 байтов. Поместим 100тыс элементов в массив (100мб — это кое-что) и вызовем qsort. Функция fcomp (функция-компаратор) сравнит нужные поля и в результате получится отсортированный массив. При этом при перестановке элементов qsort придется 3 раза копировать фрагменты по 1000 байтов. А теперь «маленькая хитрость» — создадим массив из 100тыс ссылок на исходные элементы и передадим в qsort начало этого массива ссылок. Поскольку ссылка занимает 4 байта (в 64 битных 8), а не 1000, то при обмене ссылок qsort надо поменять эти 4/8 байтов. Разумеется, нужно будет изменить fcomp, поскольку в качестве параметров она теперь получит не адреса элементов, а адреса адресов элементов (но это несложное изменение). Зато теперь можно сделать несколько функций сортировки (каждая сортирует по своему полю структуры). И даже, при необходимости, можно сделать несколько массивов ссылок. Вот сколько возможностей дает qsort!
Кстати: использование ссылок на объекты вместо самих объектов может быть полезно не только при вызове qsort, но и при применении таких контейнеров как vector, set или map.
Быстрая сортировка
Введение
Постановка задачи
Традиционно стоит начать изложение решений задачи с ее постановки. Обычно задача сортировки предполагает упорядочивание некоторого массива целых чисел по возрастанию. Но на самом деле, это является некоторым упрощением. Излагаемые в этом разделе алгоритмы можно применять для упорядочивания массива любых объектов, между которыми установлено отношение порядка (то есть про любые два элемента можно сказать: первый больше второго, второй больше первого или они равны). Упорядочивать можно как по возрастанию, так и по убыванию. Мы же воспользуемся стандартным упрощением.
Быстрая сортировка
В прошлый раз мы поговорили о чуть более сложной сортировке — сортировке вставками. Сегодня речь пойдет о существенно более сложном алгоритме — быстрой сортировке (еще ее называют сортировкой Хоара).
Описание алгоритма
Алгоритм быстрой сортировки является рекурсивным, поэтому для простоты процедура на вход будет принимать границы участка массива от l включительно и до r не включительно. Понятно, что для того, чтобы отсортировать весь массив, в качестве параметра l надо передать 0, а в качестве r — n, где по традиции n обозначает длину массива.
В основе алгоритма быстрой сортировке лежит процедура partition. Partition выбирает некоторый элемент массива и переставляет элементы участка массива таким образом, чтобы массив разбился на 2 части: левая часть содержит элементы, которые меньше этого элемента, а правая часть содержит элементы, которые больше или равны этого элемента. Такой разделяющий элемент называется пивотом.
Пивот в нашем случае выбирается случайным образом. Такой алгоритм называется рандомизированным. На самом деле пивот можно выбирать самым разным образом: либо брать случайный элемент, либо брать первый / последний элемент учаcтка, либо выбирать его каким-то «умным» образом. Выбор пивота является очень важным для итоговой сложности алгоритма сортировки, но об этом несколько позже. Сложность же процедуры partition — O(n), где n = r — l — длина участка.
Теперь используем partition для реализации сортировки:
Крайний случай — массив из одного элемента обладает свойством упорядоченности. Если массив длинный, то применяем partition и вызываем процедуру рекурсивно для двух половин массива.
Если прогнать написанную сортировку на примере массива 1 2 2, то можно заметить, что она никогда не закончится. Почему так получилось?
При написании partition мы сделали допущение — все элементы массива должны быть уникальны. В противном случае возвращаемое значение m будет равно l и рекурсия никогда не закончится, потому как sort(l, m) будет вызывать sort(l, l) и sort(l, m). Для решения данной проблемы надо массив разделять не на 2 части ( = pivot), а на 3 части ( pivot) и вызывать рекурсивно сортировку для 1-ой и 3-ей частей.
Анализ
Предлагаю проанализировать данный алгоритм.
Временная сложность алгоритма выражается через нее же по формуле: T(n) = n + T(a * n) + T((1 — a) * n). Таким образом, когда мы вызываем сортировку массива из n элементов, тратится порядка n операций на выполнение partition’а и на выполнения себя же 2 раза с параметрами a * n и (1 — a) * n, потому что пивот разделил элемент на доли.
В лучшем случае a = 1 / 2, то есть пивот каждый раз делит участок на две равные части. В таком случае: T(n) = n + 2 * T(n / 2) = n + 2 * (n / 2 + 2 * T(n / 4)) = n + n + 4 * T(n / 4) = n + n + 4 * (n / 4 + 2 * T(n / 8)) = n + n + n + 8 * T(n / 8) =…. Итого будет log(n) слагаемых, потому как слагаемые появляются до тех пор, пока аргумент не уменьшится до 1. В результате T(n) = O(n * log(n)).
В худшем случае a = 1 / n, то есть пивот отсекает ровно один элемент. В первой части массива находится 1 элемент, а во второй n — 1. То есть: T(n) =n + T(1) + T(n — 1) = n + O(1) + T(n — 1) = n + O(1) + (n — 1 + O(1) + T(n — 2)) = O(n^2). Квадрат возникает из-за того, что он фигурирует в формуле суммы арифметической прогрессии, которая появляется в процессе расписывания формулы.
В среднем в идеале надо считать математическое ожидание различных вариантов. Можно показать, что если пивот делит массив в отношении 1:9, то итоговая асимптотика будет все равно O(n * log(n)).
Сортировка называется быстрой, потому что константа, которая скрывается под знаком O на практике оказывается достаточно небольшой, что привело к широкому распространению алгоритма на практике.
Сравнение алгоритмов сортировки
В данной статье рассматриваются алгоритмы сортировки массивов. Для начала представляются выбранные для тестирования алгоритмы с кратким описанием их работы, после чего производится непосредственно тестирование, результаты которого заносятся в таблицу и производятся окончательные выводы.
Алгоритмы сортировок очень широко применяются в программировании, но иногда программисты даже не задумываются какой алгоритм работает лучше всех (под понятием «лучше всех» имеется ввиду сочетание быстродействия и сложности как написания, так и выполнения).
В данной статье постараемся это выяснить. Для обеспечения наилучших результатов все представленные алгоритмы будут сортировать целочисленный массив из 200 элементов. Компьютер, на котором будет проводится тестирование имеет следующие характеристики: процессор AMD A6-3400M 4×1.4 GHz, оперативная память 8 GB, операционная система Windows 10 x64 build 10586.36.
Для проведения исследования были выбраны следующие алгоритмы сортировки:
Selection sort (сортировка выбором) – суть алгоритма заключается в проходе по массиву от начала до конца в поиске минимального элемента массива и перемещении его в начало. Сложность такого алгоритма O(n2).
Bubble sort (сортировка пузырьком) – данный алгоритм меняет местами два соседних элемента, если первый элемент массива больше второго. Так происходит до тех пор, пока алгоритм не обменяет местами все неотсортированные элементы. Сложность данного алгоритма сортировки равна O(n^2).
Insertion sort (сортировка вставками) – алгоритм сортирует массив по мере прохождения по его элементам. На каждой итерации берется элемент и сравнивается с каждым элементом в уже отсортированной части массива, таким образом находя «свое место», после чего элемент вставляется на свою позицию. Так происходит до тех пор, пока алгоритм не пройдет по всему массиву. На выходе получим отсортированный массив. Сложность данного алгоритма равна O(n^2).
Quick sort (быстрая сортировка) – суть алгоритма заключается в разделении массива на два под-массива, средней линией считается элемент, который находится в самом центре массива. В ходе работы алгоритма элементы, меньшие чем средний будут перемещены в лево, а большие в право. Такое же действие будет происходить рекурсивно и с под-массива, они будут разделяться на еще два под-массива до тех пор, пока не будет чего разделать (останется один элемент). На выходе получим отсортированный массив. Сложность алгоритма зависит от входных данных и в лучшем случае будет равняться O(n×2log2n). В худшем случае O(n^2). Существует также среднее значение, это O(n×log2n).
Comb sort (сортировка расческой) – идея работы алгоритма крайне похожа на сортировку обменом, но главным отличием является то, что сравниваются не два соседних элемента, а элементы на промежутке, к примеру, в пять элементов. Это обеспечивает от избавления мелких значений в конце, что способствует ускорению сортировки в крупных массивах. Первая итерация совершается с шагом, рассчитанным по формуле (размер массива)/(фактор уменьшения), где фактор уменьшения равен приблизительно 1,247330950103979, или округлено до 1,3. Вторая и последующие итерации будут проходить с шагом (текущий шаг)/(фактор уменьшения) и будут происходить до тех пор, пока шаг не будет равен единице. Практически в любом случае сложность алгоритма равняется O(n×log2n).
Для проведения тестирования будет произведено по 5 запусков каждого алгоритма и выбрано наилучшее время. Наилучшее время и используемая при этом память будут занесены в таблицу. Также будет проведено тестирование скорости сортировки массива размером в 10, 50, 200 и 1000 элементов чтобы определить для каких задач предназначен конкретный алгоритм.
Полностью неотсортированный массив:
Частично отсортированный массив (половина элементов упорядочена):
Результаты, предоставленые в графиках:
В результате проведенного исследования и полученных данных, для сортировки неотсортированного массива, наиболее оптимальным из представленных алгоритмов для сортировки массива является быстрая сортировка. Несмотря на более длительное время выполнения алгоритм потребляет меньше памяти, что может быть важным в крупных проектах. Однако такие алгоритмы как сортировка выбором, обменом и вставками могут лучше подойти для научных целей, например, в обучении, где не нужно обрабатывать огромное количество данных. При частично отсортированном массиве результаты не сильно отличаются, все алгоритмы сортировки показывают время примерно на 2-3 миллисекунды меньше. Однако при сортировке частично отсортированного массива быстрая сортировка срабатывает намного быстрее и потребляет меньшее количество памяти.
Какой алгоритм сортировки быстрее?
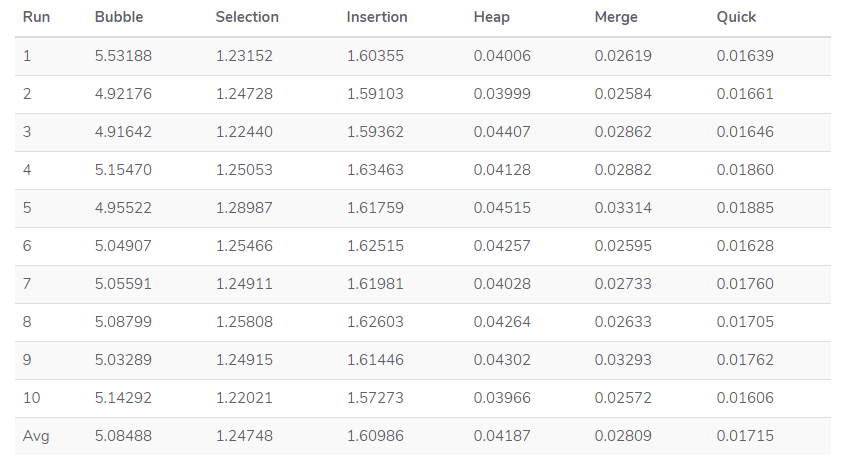
Существует много видов сортировки: пузырьковая (bubble), выборкой (Selection), вставками (Insertion), куча (Heap), слиянием (Merge), быстрая (Quick). В этой статье мы постараемся определить, какой из этих алгоритмов быстрее.
Для решения поставленной задачи сгенерируем массив в Python, состоящий из пяти тысяч чисел от 0 до 1000. Потом определим время, нужное нам для завершения каждого алгоритма. И повторим каждый метод десять раз, дабы можно было точнее определить производительность.
Что получили?
Самым медленным алгоритмом оказалась пузырьковая сортировка. Возможно, она будет полезна при ознакомлении с темой алгоритмов сортировки, однако всё же Bubble Sort — не самый лучший вариант для практического применения.
А вот быстрая сортировка неплохо оправдала своё название, показав скорость, которая почти в 2 раза выше, чем при сортировке слиянием. При этом нам не потребуется дополнительное место для результирующего массива.
Идём дальше. Сортировка вставками при своей работе выполняет меньше сравнений, если сравнивать с сортировкой выборкой. Таким образом, в реальности Insertion Sort должна быть более производительна. Однако в нашем случае она сработала чуть-чуть медленней. Всё дело в том, что сортировка вставками выполняет намного больше обменов элементами. А когда эти обмены занимают гораздо больше времени, чем сравнение самих элементов, полученный в нашем эксперименте результат является закономерным.
Напоследок, добавим, что лучше понять вышеупомянутые алгоритмы поможет их визуализация. При этом масштаб сравнения и число перестановок, которые выполняет алгоритм совместно со средой выполнения кода, как раз таки и будут главными факторами, определяющими производительность. Что касается реальных приложений на Python, то мы рекомендуем применять встроенные функции сортировки, так как они реализованы с учётом удобства разработчика.
Timsort — самый быстрый алгоритм сортировки, о котором вы никогда не слышали
Timsort: Очень быстрый, O(n log n), стабильный алгоритм сортировки, созданный для реального мира, а не для академических целей.
Timsort — это алгоритм сортировки, который эффективен для реальных данных, а не создан в академической лаборатории. Tim Peters создал Timsort для Python в 2001 году.
Timsort сначала анализирует список, который он пытается отсортировать, и на его основе выбирает наилучший подход. С момента его появления он используется в качестве алгоритма сортировки по умолчанию в Python, Java, платформе Android и GNU Octave.
Нотация Big O для Timsort — это O(n log n). Чтобы узнать о нотации Big O, прочтите это.
Время сортировки Timsort такое же, как и у Mergesort, что быстрее, чем у большинства других известных сортировок. Timsort фактически использует сортировку вставкой как и Mergesort. Вы это скоро увидите.
Peters разработал Timsort для использования уже упорядоченных элементов, которые существуют в большинстве реальных наборов данных. Он называет эти упорядоченные элементы «natural runs» (естественные пробеги). Они итеративно перебирают данные, собирая элементы в пробеги и одновременно объединяя несколько этих пробегов в один.
Если массив (array), который мы пытаемся отсортировать, содержит менее 64 элементов, Timsort выполняет сортировку вставкой.
Сортировка вставкой — это простая сортировка, которая наиболее эффективна для небольших списков. Она функционирует довольно медленно при работе с большими списками, но при этом быстро работает с маленькими списками. Идея сортировки вставкой заключается в следующем:
Просматривать элементы по одному
Построить отсортированный список, вставляя элемент в нужное место
Вот таблица, показывающая, как сортировка вставкой сортирует список [34, 10, 64, 51, 32, 21].
В данном случае мы вставляем только что отсортированные элементы в новый подмассив (sub-array), который начинается от начала массива.
Вот gif, показывающий сортировку вставкой:
Больше о пробегах
Если список больше 64 элементов, то алгоритм сделает первый проход (pass) по списку в поисках частей, которые строго возрастают или убывают. Если какая-либо часть является убывающей, то она будет изменена.
Таким образом, если пробег уменьшается, он будет выглядеть следующим образом (пробег выделен жирным шрифтом):
Если не происходит уменьшение, то это будет выглядеть следующим образом:
Алгоритм выбирает minrun из диапазона от 32 до 64 включительно, таким образом, чтобы длина исходного массива при расчете была меньше или равна степени числа 2.
Если длина пробега меньше minrun, необходимо рассчитать длину этого пробега относительно minrun. Используя это новое число выполняется сортировка вставкой для создания нового пробега.
Итак, если minrun равен 63, а длина пробега равна 33, вы выполняете вычитание: 63-33 = 30. Затем вы берете 30 элементов из run[33], и делаете сортировку вставкой для создания нового пробега.
После завершения этой части должно появиться множество отсортированных пробегов в списке.
Слияние
Теперь Timsort использует сортировку слиянием, чтобы объединить пробеги. Однако Timsort следит за тем, чтобы сохранить стабильность и баланс слияния во время сортировки.
Для поддержания стабильности мы не должны менять местами два одинаковых числа. Это не только сохраняет их исходные позиции в списке, но и позволяет алгоритму работать быстрее. В ближайшее время мы обсудим баланс слияния.
Когда Timsort находит пробеги, он добавляет их в стек. Простой стек выглядит следующим образом:
Представьте себе стопку тарелок. Вы не можете взять тарелки снизу, поэтому вам приходится брать их сверху. То же самое можно сказать и о стеке.
Timsort пытается сбалансировать две конкурирующие задачи при сортировке слиянием. С одной стороны, мы хотели бы отложить слияние на как можно дольше, чтобы использовать паттерны, которые могут появиться позже, но еще больше нам хотелось бы произвести слияние как можно быстрее, чтобы воспользоваться тем, что только что найденный пробег все еще находится наверху в иерархии памяти. Мы также не можем откладывать слияние «слишком надолго», потому что на запоминание еще не объединенных пробегов расходуется память, а стек имеет фиксированный размер.
Чтобы добиться компромисса, Timsort отслеживает три последних элемента в стеке и создает два правила, которые должны выполняться для этих элементов:
По словам Tim Peters:
Обычно объединить соседние пробеги разной длины очень сложно. Еще сложнее то, что мы должны поддерживать стабильность. Чтобы обойти эту проблему, Timsort выделяет временную память. Он помещает меньший (называя оба пробега A и B) из двух побегов в эту временную память.
Galloping*
*Модификация процедуры слияния подмассивов
Пока Timsort объединяет A и B, обнаруживается, что один пробег «выигрывает» много раз подряд. Если бы оказалось, что A состоял из гораздо меньших чисел, чем B, то A оказался бы на прежнем месте. Слияние этих двух пробегов потребовало бы много работы c нулевым результатом.
Чаще всего данные имеют некоторую уже существующую внутреннюю структуру. Timsort предполагает, что если многие значения пробега A меньше, чем значения пробега B, то, скорее всего, A будет и дальше содержать меньшие значения, чем B.
Затем Timsort переходит в режим galloping. Вместо того чтобы сверять A[0] и B[0] друг с другом, Timsort выполняет бинарный поиск соответствующей позиции b[0] в a[0]. Таким образом, Timsort может полностью переместить A. Затем Timsort ищет соответствующее местоположение A[0] в B. После этого Timsort также может полностью перемещает B.
Давайте посмотрим на это в действии. Timsort проверяет B[0] (который равен 5) и, используя бинарный поиск, ищет соответствующее место в A.
Оказывается, что действие не имеет смысла, если подходящее место для B[0] находится очень близко к началу A (или наоборот), поэтому режим gallop быстро завершается, если он не приносит результатов. Кроме того, Timsort принимает это к сведению и усложняет вход в режим gallop, увеличивая количество последовательных «побед» только в A или только в B. Если режим gallop приносит результаты, Timsort облегчает его повторный запуск.
Если говорить коротко, Timsort делает две вещи невероятно хорошо:
Обеспечивает высокую производительность при работе с массивами с уже существующей внутренней структурой
Создает возможность поддерживать стабильную сортировку
А раньше, чтобы добиться стабильной сортировки, вам нужно было сжать элементы списка в целые числа и отсортировать его как массив кортежей.
Если вас не интересует код, смело пропускайте эту часть. Под этим разделом есть дополнительная информация.
Если вы хотите увидеть оригинальный исходный код Timsort во всей его красе, посмотрите его здесь. Timsort официально реализован на C, а не на Python.
Timsort фактически встроен прямо в Python, поэтому этот код служит только в качестве пояснения. Чтобы использовать Timsort, просто напишите следующее:
Если вы хотите узнать, как работает Timsort, и понять его суть, я настоятельно рекомендую вам попробовать применить его самостоятельно!
Эта статья основана на оригинальном вступлении Tim Peters к Timsort, которое можно найти здесь.
Если вам интересно узнать о курсе больше, приглашаем на день открытых дверей онлайн.