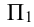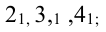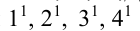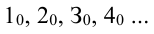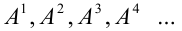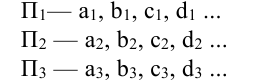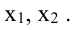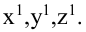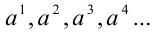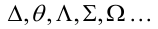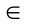какой метод проецирования называется ортогональным или прямоугольным

Какой метод проецирования называется ортогональным или прямоугольным

Описанные построения выражают суть операции, называемой центральным проецированием точек пространства на плоскость.

В евклидовом пространстве существуют точки, которые не имеют центральных проекций, и наоборот в плоскости П_i есть точки, которые в пространстве не имеют оригиналов (точки D и F).

Точка D_i проекции прямой m_i не имеет оригинала на прямой m, так как проецирующий луч SD_i параллелен прямой.

Для исключения подобных случаев евклидово пространство расширяют введением несобственных (бесконечно удаленных) точек. Такое пространство называется расширенным евклидовым пространством.

Проецирующие лучи, проведенные через все точки кривой n , образуют проецирующую коническую поверхность N (рис.2). Проекция криволинейной фигуры, таким образом, представляет собой линию пересечения проецирующей поверхности N и плоскости проекций П _i .

Рисунок 2. Центральное проецирование линии

Рисунок 3. Центральное проецирование поверхности

Центральное проецирование есть наиболее общий случай проецирования геометрических объектов на плоскости.

Основными и неизменными его свойствами (инвариантами) являются следующие:

1) проекция точки – точка;

2) проекция прямой – прямая;

3) если точка принадлежит прямой, то проекция этой точки принадлежит проекции прямой.

По принципу центрального проецирования работают фотоаппараты и кинокамеры. Упрощенная схема работы человеческого глаза близка к этому виду проецирования: роль центра проецирования выполняет оптический центр хрусталика, роль проецирующих прямых – лучи света; плоскостью проекций служит сетчатка глаза. Поэтому изображения, построенные по принципу центрального проецирования, наиболее наглядны и их широко используют в своей работе художники, архитекторы, дизайнеры и многие другие специалисты.

Частный случай центрального проецирования – параллельное проецирование , когда центр проецирования удален в бесконечность, при этом проецирующие лучи можно рассматривать как параллельные проецирующие прямые. Положение проецирующих прямых относительно плоскости проекций определяется направлением проецирования S (рис.4). В этом случае полученное изображение называют параллельной проекцией объекта.

При параллельном проецировании сохраняются свойства центрального и добавляются следующие:

проекции параллельных прямых параллельны между собой;

отношение отрезков прямой равно отношению их проекций;

отношение отрезков двух параллельных прямых равно отношению их проекций.

Рисунок 4. Параллельное проецирование

Прямоугольное (ортогональное) проецирование является частным случаем параллельного.

Проекция объекта, полученная с использование этого метода, называется ортогональной .

Ортогональному проецированию присущи все свойства параллельного и центрального проецирования и кроме того, справедлива теорема о проецировании прямого угла: если хотя бы одна сторона прямого угла параллельна плоскости проекций, а вторая не перпендикулярна ей, то прямой угол на эту плоскость проецируется в прямой угол .

К проекционным изображениям в начертательной геометрии предъявляются следующие основные требования:

1. Обратимость – восстановление оригинала по его проекционным изображениям (чертежу) – возможность определять форму и размеры объекта, его положение и связь с окружающей средой.

2. Наглядность – чертеж должен создавать пространственное представление о форме предмета.

3. Точность – графические операции, выполненные на чертеже, должны давать достаточно точные результаты.

4. Простота – изображение должно быть простым по построению и допускать однозначное описание объекта в виде последовательности графических операций.

Источник

Какой метод проецирования называется ортогональным или прямоугольным

Описанные построения выражают суть операции, называемой центральным проецированием точек пространства на плоскость.

В евклидовом пространстве существуют точки, которые не имеют центральных проекций, и наоборот в плоскости П_i есть точки, которые в пространстве не имеют оригиналов (точки D и F).

Точка D_i проекции прямой m_i не имеет оригинала на прямой m, так как проецирующий луч SD_i параллелен прямой.

Для исключения подобных случаев евклидово пространство расширяют введением несобственных (бесконечно удаленных) точек. Такое пространство называется расширенным евклидовым пространством.

Проецирующие лучи, проведенные через все точки кривой n , образуют проецирующую коническую поверхность N (рис.2). Проекция криволинейной фигуры, таким образом, представляет собой линию пересечения проецирующей поверхности N и плоскости проекций П _i .

Рисунок 2. Центральное проецирование линии

Рисунок 3. Центральное проецирование поверхности

Центральное проецирование есть наиболее общий случай проецирования геометрических объектов на плоскости.

Основными и неизменными его свойствами (инвариантами) являются следующие:

1) проекция точки – точка;

2) проекция прямой – прямая;

3) если точка принадлежит прямой, то проекция этой точки принадлежит проекции прямой.

По принципу центрального проецирования работают фотоаппараты и кинокамеры. Упрощенная схема работы человеческого глаза близка к этому виду проецирования: роль центра проецирования выполняет оптический центр хрусталика, роль проецирующих прямых – лучи света; плоскостью проекций служит сетчатка глаза. Поэтому изображения, построенные по принципу центрального проецирования, наиболее наглядны и их широко используют в своей работе художники, архитекторы, дизайнеры и многие другие специалисты.

Частный случай центрального проецирования – параллельное проецирование , когда центр проецирования удален в бесконечность, при этом проецирующие лучи можно рассматривать как параллельные проецирующие прямые. Положение проецирующих прямых относительно плоскости проекций определяется направлением проецирования S (рис.4). В этом случае полученное изображение называют параллельной проекцией объекта.

При параллельном проецировании сохраняются свойства центрального и добавляются следующие:

проекции параллельных прямых параллельны между собой;

отношение отрезков прямой равно отношению их проекций;

отношение отрезков двух параллельных прямых равно отношению их проекций.

Рисунок 4. Параллельное проецирование

Прямоугольное (ортогональное) проецирование является частным случаем параллельного.

Проекция объекта, полученная с использование этого метода, называется ортогональной .

Ортогональному проецированию присущи все свойства параллельного и центрального проецирования и кроме того, справедлива теорема о проецировании прямого угла: если хотя бы одна сторона прямого угла параллельна плоскости проекций, а вторая не перпендикулярна ей, то прямой угол на эту плоскость проецируется в прямой угол .

К проекционным изображениям в начертательной геометрии предъявляются следующие основные требования:

1. Обратимость – восстановление оригинала по его проекционным изображениям (чертежу) – возможность определять форму и размеры объекта, его положение и связь с окружающей средой.

2. Наглядность – чертеж должен создавать пространственное представление о форме предмета.

3. Точность – графические операции, выполненные на чертеже, должны давать достаточно точные результаты.

4. Простота – изображение должно быть простым по построению и допускать однозначное описание объекта в виде последовательности графических операций.

Источник

Какой метод проецирования называется ортогональным или прямоугольным

1.1. ЦЕНТРАЛЬНОЕ ПРОЕЦИРОВАНИЕ.
ПОНЯТИЕ О ПРОЕКТИВНОМ ПРОСТРАНСТВЕ

Для того чтобы построить проекцию некоторой точки А, выбирается произвольная плоскость П₁, называемая плоскостью проекций, и точка S, не принадлежащая плоскости П₁, называемая центром проекций (рис. 1.1).

1. Проекция точки на плоскость есть точка (рис. 1.4)

A A₁.

2. Проекция прямой в общем случае прямая: l l₁, (рис. 1.6); она вырождается в точку, если прямая параллельна направлению проецирования:

3. Если точка принадлежит линии, то проекция точки принадлежит проекции линии (рис. 1.6):

A l A₁ l₁

Следствие из пп. 2 и 3. Для построения проекции прямой достаточно построить проекции двух принадлежащих ей точек (рис. 3):

A l B l A₁ l₁ B_l l₁

4. Точка пересечения линий проецируется в точку пересечения их проекций (рис. 1.6):

К = а b K₁ = а₁ b₁

5. Проекции параллельных прямых параллельны (рис. 1.7):

l l’ l₁ l₁‘

Следствия:
1) отношение длин отрезков параллельных прямых равно отношению длин их проекций (рис. 1.7):

2) если точка, принадлежащая отрезку прямой, делит его в некотором отношении, то проекция точки делит проекцию отрезка в том же отношении (рис. 1.6):

6. Если геометрическая фигура Ф принадлежит плоскости , параллельной плоскости проекций (например, П₁), то проекция этой фигуры на плоскость П₁ конгруэнтна самой фигуре:

Например, если отрезок МN параллелен плоскости проекций, то его проекция на данную плоскость конгруэнтна самому отрезку (рис. 1.7):

Рис. 1.8 (анимационный)

Внимание:
Подумайте, проанализируйте чертежи и докажите справедливость перечисленных инвариантов параллельного проецирования. Рассмотренные свойства (инварианты) параллельного проецирования сохраняются при любом направлении проецирования.

Примечание.
Метрические характеристики геометрических фигур при параллельном проецировании в общем случае не сохраняются (происходит искажение линейных и угловых величин).

Если направление проецирования перпендикулярно плоскости проекций, параллельное проецирование называется ортогональным (прямоугольным)
s П₁ (AA₁) П₁. В этом случае проекция А₁, точки А называется ортогональной, или прямоугольной (рис. 1.9). В противном случае проецирование называется косоугольным.

Ортогональное проецирование, являясь частным случаем параллельного, значительно упрощает построение проекций геометрических фигур и является основным при выполнении комплексных чертежей технических форм (рис. 1.10). Рассмотренные в предыдущих параграфах однопроекционные чертежи геометрических фигур являются необратимыми.

Источник

Образование проекций в начертательной геометрии с примерами

Содержание:

В любой отрасли промышленности для изготовления отдельных деталей и составных частей машин создаются их геометрические (идеальные) образы, которые называются чертежами. Под чертежами понимают плоское изображение геометрических очертаний и размеров технического объекта, выполненное таким образом, чтобы можно было представить его объёмные формы.

У будущего инженера важно выработать и развить пространственное (объемное) «видение» плоского изображения. Это позволяет не только правильно читать и понимать плоские чертежи, но и, используя целый ряд правил и положений, грамотно их выполнять. Все эти вопросы рассматриваются студентами вузов при изучении первой общепрофессиональной дисциплины «Инженерная графика».

Важнейшей составной частью является курс начертательной геометрии, который в силу его большой значимости во многих образовательных стандартах выделен в отдельную дисциплину.

Изучение этого курса преследует следующие основные цели:

В отличие от других изданий лекционный курс минимизирован до объема, предусмотренного рабочей программой по начертательной геометрии для студентов специальности 190701 и 181400, достаточного для самостоятельной работы студента, выполнения им графических заданий.

Рекомендуется для студентов родственных специальностей, изучающих курс начертательной геометрии и обучаемых в ВУЗах министерства транспорта Российской Федерации.

При изучении курса приняты следующие обозначения:

1.1. Плоскости проекций: горизонтальная —

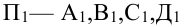
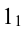
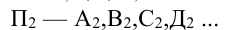
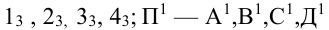
1.3. Проекции точек на плоскость: . или , или или или

1.4. Точки на развертках: 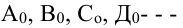или

1.5. Последовательный ряд точек:

1.7. Проекции линий на плоскость:

1.9. Координатные оси проекций:

1.10. Новые оси абсцисс, полученные при замене плоскостей проекций:

1.11. Аксонометрические оси координат:

1.12. Последовательный ряд линий:

1.13. Прямая, проходящая через точки А и В: АВ.

1.14. Плоскости (поверхности):

1.15. Знак принадлежности

1.16. Знак совпадения ≡

Образование проекций и методы проецирования

Плоский чертеж какого-либо технического объекта может состоять из нескольких изображений, по которым и создается представление об объемных формах объекта. Такие плоские изображения называются проекциями рассматриваемого объекта.

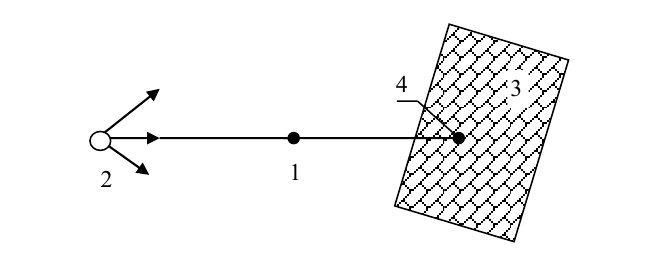
Под проекцией любой точки понимают ее как бы «теневое» отображение на какой-либо плоскости. Так, если поместить материальную точку 1 между источниками света (световых лучей) 2 и какой-либо плоскостью 3 (рис. 2.1), на этой плоскости увидим тень 4 этой точки, которую и принято называть проекцией точки.

Взаимное положение источника света и плоскости может быть произвольным. В зависимости от величины угла между лучом 2-1-4 и плоскостью 3 возможны два принципиально отличных варианта проекций точки:

Курс начертательной геометрии рассматривает два основных метода проецирования: центральный и параллельный.

Метод центрального проецирования

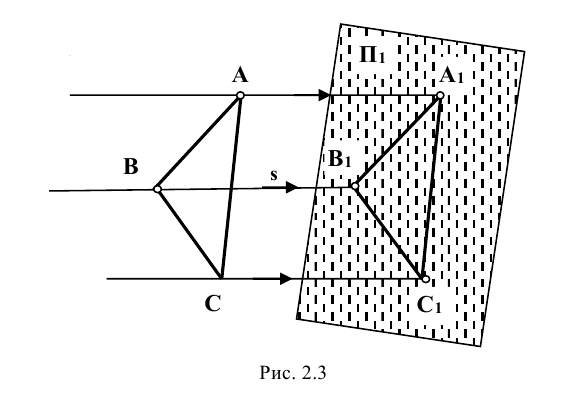
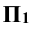
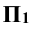
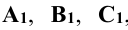
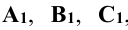
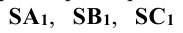
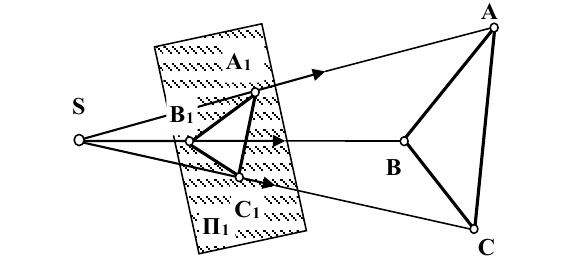
Суть метода заключается в следующем: пусть даны в пространстве треугольник ABC, плоскость и произвольная точка S (рис. 2.2). Проведя из точки S прямые линии (лучи) через вершины треугольника ABC до пересечения их с плоскостью , получают точки . Эти точки называют центральными проекциями точек А, В, С. Соединив прямыми линиями точки , получают центральную проекцию треугольника ABC. Точка S называется центром проецирования, плоскость — плоскостью проекций, лучи — проецирующими лучами. Рис. 2.2

Метод параллельного проецирования

Если точку S удалить от плоскости в бесконечность, проецирующие лучи будут практически параллельны между собой. Тогда они пересекутся с плоскостью проекций в точках , которые называются параллельными проекциями точек А, В, С. Соединив, как и в предшествующем случае, точки между собой, получают треугольник , который будет уже параллельной проекцией треугольника ABC. На рис. 2.3 стрелкой s обозначено направление проецирования. Если направление s перпендикулярно к плоскости , то проекция треугольника называется параллельной прямоугольной или ортогональной.

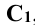
Если направление луча s не перпендикулярно к плоскости , то проекция треугольника называется косоугольной.

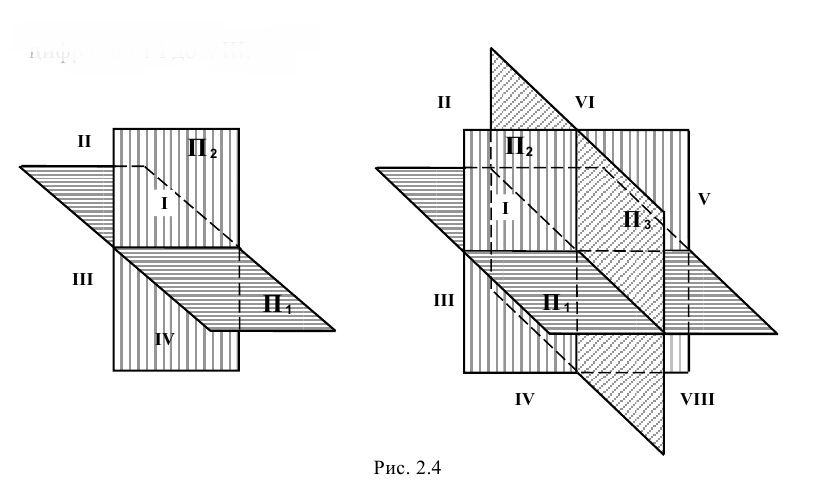
Система плоскостей проекций в практике решения инженерных задач

Они соответственно получили обозначения: горизонтальная плоскость проекций – , и фронтальная — . Эти плоскости пересекаются между собой под прямым углом, образуя линию пересечения — ось х, и делят пространство на четыре четверти (квадранты), которые принято обозначать римскими цифрами I, II, III и IV (рис. 2.4).

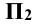
В случае недостаточной информативности об объекте по двум проекциям на указанные плоскости и используют третью плоскость , перпендикулярную плоскостям и . Она называется профильной плоскостью проекций. Плоскость пересекается с плоскостью образуя ось у, и с плоскостью , образуя ось z.

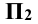
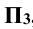
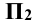
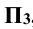
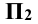
Указанные плоскости делят всё пространство вокруг уже на восемь частей, которые называются октантами и обозначаются римскими цифрами от I до VIII.

При копировании любых материалов с сайта evkova.org обязательна активная ссылка на сайт www.evkova.org

Сайт создан коллективом преподавателей на некоммерческой основе для дополнительного образования молодежи

Сайт пишется, поддерживается и управляется коллективом преподавателей

Whatsapp и логотип whatsapp являются товарными знаками корпорации WhatsApp LLC.

Cайт носит информационный характер и ни при каких условиях не является публичной офертой, которая определяется положениями статьи 437 Гражданского кодекса РФ. Анна Евкова не оказывает никаких услуг.

Источник