какой метод положен в основу компьютерной модели эпидемии

Математические модели эпидемического процесса.

Математической моделью называют абстрактную модель, в которой реальные объекты исследования заменяются

идеальными и описываются при помощи математических соотноше-

ний или различных алгоритмических схем.

Моделирование следует рассматривать как важнейший инструмент познания эпидемического процесса. Широкое использование терминов «модель», «математическая модель» и самих моделей в эпидемиологии знаменует шаг вперед по сравнению с классическими методологическими установками.

Моделирование эпидемического процесса имеет свою историю, причем главные ее страницы связаны с математическими моделями.

1) формальную апроксимацию (приближение), состоящую в перенесении знаний математического описания внешне подобных явлений из других областей (например, волновых колебаний) на эпидемический процесс;

2) формальную экстраполяцию (в основном кривых заболеваемости), дающую удовлетворительные результаты лишь в том случае, если факторы, формирующие рассматриваемый эпидемический процесс, примерно постоянны;

3) содержательное моделирование эпидемического процесса с дискретным или непрерывным течением.

Каждый из этих классов моделирования оперирует своим специфическим набором математических средств, имеющих определенные ограничения и показания к применению. В то же время модели, относящиеся к одному классу, обеспечивают определенный уровень отдачи при исследовании эпидемического процесса. Следовательно, между задачей и способом моделирования имеется тесная связь.

В эпидемиологии моделирование применяется в исследовательских целях, для прогнозирования характера эпидемического процесса и определения стратегии служб здравоохранения.

Познавательная роль моделей определяется их сущностью, предполагающей выявление взаимосвязей многочисленных параметров эпидемического процесса. Хорошо организованная математическая модель дисциплинирует исследовательскую работу, систематизирует научные знания и нередко приводит к появлению новых идей. Она позволяет судить о числе контактов, определять степень риска инфицирования и заболевания, исследовать особенности возрастного и территориального распределения заболеваемости. Не менее важной функцией модели является описание многолетней динамики заболеваемости, включая сезонные циклы, что открывает возможность прогнозирования тенденций и уровней развития основных показателей эпидемического процесса. Разумное использование методов математического моделирования эпидемического процесса может быть чрезвычайно полезно также при планировании профилактических и противоэпидемических мероприятий, для выбора оптимальных путей борьбы с эпидемическим распространением заболеваний.

При построении эпидемиологической модели различают несколько этапов:
— установление структуры модели на основе собранных фактических данных о параметрах эпидпроцесса (восприимчивость, устойчивость, инкубационный период, длительность болезни, бактерионосительство, продолжительность иммунитета и др.);
— математическая формулировка модели;
— «проигрывание» на ЭВМ ряда вариантов эпидпроцесса при включении различных условий, влияющих на распространение инфекции, с целью выбора оптимального.

Большинство моделей сконструировано и применено с целью краткосрочного прогнозирования заболеваемости, что, по всей вероятности, диктуется потребностями противоэпидемической службы для подготовки и своевременной реализации в практических условиях эффективных профилактических, противоэпидемических и лечебных мероприятий. Исследовательским задачам, соподчиненным с выбором оптимальной тактики борьбы с заболеваемостью, посвящено лишь незначительное число моделей.

За многие годы существования человечества огромное число людей погибло от различных эпидемий. Чума, холера, грипп и др. нередко поражали значительные массы людей. Для того, чтобы иметь возможность бороться с эпидемиями, т.е. своевременно применять те или иные медицинские мероприятия (карантины, вакцинации и т.п.),необходимо уметь сравнивать эффективность этих мероприятий. Сравнить же их можно лишь в том случае, если есть возможность предсказать, как при том или ином мероприятии будет меняться ход эпидемии, т.е. как будет меняться число заболевших.

Отсюда возникает необходимость в построении модели, которая могла бы служить целям прогноза.

Для простоты рассмотрим естественный ход эпидемии без какого-либо вмешательства и попробуем спрогнозировать последствия.

Так как нашей целью является лишь создание иллюстративной модели, то здесь мы абстрагируемся от очень многих факторов ( условия размножения бактериальных клеток, степень восприимчивости к инфекции отдельных людей, вероятность встречи носителя инфекции со здоровым человеком и т.д.)

Итак, пусть имеется N здоровых людей, и в момент времени t=0 в эту группу попадает один заболевший человек – источник инфекции. Будем предполагать, что никакого удаления заболевших из группы не происходит. Считаем также, что человек становится источником инфекции сразу же после того, как он сам заразится.

Допустим в некоторый момент времени t

X(t) – число источников инфекции,

Y(t) – число людей, могущих заболеть,

Тогда имеем X(t)+Y(t)=N+1 в любой момент времени.

При t=0 выполняется условие X(0)=1

Количество новых больных dX, появившихся за промежуток времени dt, будет пропорционально числу встреч здоровых и заболевших людей, т.е. произведению величин XY. Следовательно, можно записать

или ,

где a – коэффициент пропорциональности.

Полученное дифференциальное уравнение вместе с условием X(0)=1 определяет функцию X(t), т.е. численность заболевших в момент времени t.

Найдем общее решение, предварительно разделив переменные.

Чтобы взять первый интеграл, разделим числитель и знаменатель дроби на и введем новую переменную , тогда , и отсюда .

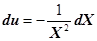
Заменим под интегралом переменную, получим

После интегрирования имеем

, и, следовательно

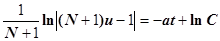
С учетом того, что ,получим искомую функцию X(t)

Так как при t=0 значение X(t)=1, то для определения величины С имеем уравнение

, откуда C=N

Итак, мы знаем число заболевших как функцию времени. Проанализируем полученную формулу. При возрастании t знаменатель дроби убывает, т. е. X(t) увеличивается. Это соответствует нашим представлениям, так как, согласно им, число заболевших может только увеличиваться.

Интересно выяснить, как меняется скорость увеличения числа больных. Для решения этого вопроса нужно изучить величину .

Числитель дроби обращается в нуль при .

Таким образом, когда , величина , а когда , величина .

Следовательно, функция — скорость возрастания числа заболевших – растет вплоть до момента , а затем убывает.

Этот результат хорошо согласуется с экспериментальными данными, так как известно, что в начале эпидемии число заболевших резко растет, а впоследствии скорость распространения инфекции снижается.

Источник

«Математическое моделирование процесса пандемии: теория и практика»

Анализ и математическое моделирование вспышек заболеваний играют важную роль в планировании ответных мер органов здравоохранения на вспышки инфекционных заболеваний, эпидемии и пандемии. Основная цель любого такого моделирования – это определение характеристик, динамики и влияния пандемий, а также оценки эффективности мероприятий в различных условиях. Тем не менее, следует учитывать, что основная информация для принимающих решения органов поступает на ежедневной основе не по результатам сложного имитационного моделирования, а из простого и проводимого в реальном времени статистического анализа, основывающегося на механистических моделях передачи, использующих доступные эпидемиологические и вирусологические данные. Математическое моделирование может только служить инструментом для обработки доступных данных и указывать, какие дополнительные сведения могут быть полезны при принятии управленческих решений. В этой небольшой статье мы рассмотрим некоторые обобщенные модели, используемые в настоящее время при моделировании процесса распространения эпидемий.

В основе современного математического моделирования эпидемий заложен принцип экспоненциального роста числа заболевших. Это означает, что рост числа заболевших с течением времени постепенно увеличивается пропорционально определенному коэффициенту, который является константой и рассчитывается для каждого заболевания отдельно. Одной из наиболее распространенных моделей является модель SEIR, в которой всё население делится на группы:

S (Susceptible) – «уязвимый»;

E (Exposed) – зараженный на стадии инкубационного периода;

I (Infected) – зараженный;

R (Recovered) – выздоровевший.

Модель описывает распространение эпидемии в популяции, в которой нет иммунитета к инфекции. Каждый заразившийся (I) имеет фиксированную вероятность выздороветь в единицу времени — то есть перейти в группу выздоровевших (R). Заражение уязвимых (S) происходит в результате «опасных» контактов с зараженными (I). При этом контакты с теми, кто находится в инкубационном периоде, то есть еще не имеет симптомов (E), могут быть как «опасными» (если человек может заражать других до появления признаков болезни) или неопасными, если человек ещё не заразен. В основе модели SEIR два параметра: t – типичное время от заражения до выздоровления и R₀ — коэффициент воспроизводства (его можно понимать как среднее число людей, которых один зараженный успевает заразить за время, пока сам не выздоровеет). Значение t можно представить как сумму разных периодов: инкубационного периода до наступления симптомов (его «заразной» и «незаразной» частей) и времени между первыми проявлениями болезни и выздоровлением. А R₀ — как сумму разных типов заражения: через контакты людей с симптомами и без симптомов или через окружающую среду (зараженные поверхности). R₀ является расчетной величиной (напрямую выявить её можно, только исследовав историю заражения каждого человека в популяции). Обычно R₀ рассчитывается из скорости роста числа новых выявленных зараженных. R₀ может быть разным в разных популяциях и на разных стадиях эпидемии: его значение зависит от принятых мер по подавлению эпидемии, которые прерывают цепочки передачи вируса (различные формы карантина, выявление заразившихся и отслеживание их контактов).

Формула для расчета:

R₀ = (1 + (𝜏ₑ/𝜏₂)ln2) (1 + (𝜏ᵢ/𝜏₂)ln2),

где 𝜏 — средняя длина инкубационного периода, а 𝜏ᵢ — заразного периода (ln2 ≈ 0,693 — это натуральный логарифм двух).

Таким образом, при R₀ 1 – она распространяется и охватывает существенную часть населения. Например, при R₀ = 2 общее число переболевших оказывается равно примерно 80 %. Это значит, что в случае, когда R₀ существенно больше единицы, эпидемия остановится только тогда, когда значительная доля населения переболеет и приобретет иммунитет (так называемый групповой иммунитет): доля уязвимых (S) снизится настолько, что у вируса больше не будет достаточно «целей» для распространения.

Для модели SEIR критически важны сведения о темпах роста реального числа зараженных. Основной показатель моделей — R₀, это среднее количество заразившихся от одного инфицированного в условиях отсутствия мер сдерживания. Он рассчитывается на основе данных о времени удвоения числа инфицированных; чтобы знать время удвоения, нужно знать суточные темпы роста числа реально зараженных. Пока не удастся установить долю «неучтенных» в каждой стране или городе (и изменение этой доли со временем), модели получаются слишком грубыми: с их помощью можно уловить лишь общие тенденции и сделать общие выводы – например, нужны ли уже в данной области меры сдерживания эпидемии.

В настоящее время набирают популярность так называемые методы имитационного моделирования и агентного подхода. Сущность имитационного моделирования заключается в том, что для исследуемой системы (развития эпидемии) строятся графические диаграммы связей и глобальных влияний одних параметров на другие во времени. Созданная на основе этих диаграмм модель имитируется на компьютере (одним из программных продуктов позволяющих это сделать является программа AnyLogic). Такой вид моделирования позволяет проникнуть в суть происходящего в системе и выявить причинно-следственные связи между объектами и явлениями. Целью агентного моделирования является получение представления об этих глобальных правилах, общем поведении системы, исходя из предположений об индивидуальном, частном поведении её отдельных активных объектов и взаимодействии этих объектов в системе. Именно такой метод был применен китайскими учеными для моделирования эпидемии коронавируса в Китае.

Агентное моделирование (АМ) используется для моделирования действий и взаимодействий агентов с персонализированными свойствами и поведением. Оно находит широкое применение во многих сферах, включая биологию, экологию и социологию. Поскольку, как отмечают китайские исследователи, распространение 2019-nCoV – это относительно сложный процесс, получение соответствующих параметров для построения модели АМ затруднительно. Поэтому в модели сложный процесс распространения 2019-nCoVбыл до некоторой степени упрощен. Человек, представленный в виде агента – основа этой имитационной модели. Исследование предполагает, что статус каждого человека в модели можно разделить на 4 вида: уязвимый, инфицированный, заболевший и с приобретенным иммунитетом (классическая модель SEIR). В исследовании было сделано предположение, что:

Для исследования в модели была создана простая интерактивная среда. Было выдвинуто предположение, что человек постоянно находится дома или в общественных местах. До появления симптомов болезни (то есть человек не инфицирован или находится в инкубационном периоде) он обычно выходит из дома, направляясь в общественное место, а после этого возвращается обратно. Чтобы имитировать тенденцию распространения эпидемии 2019-nCoV, в модели существовали 10000 человек, один из которых был случайно заражен. Модель запускалась 10 раз, и средние значения показателей были взяты как результат эксперимента. Полученные данные были отсортированы и откорректированы с помощью программы R3.6.2, а модель создавалась на основе ПО AnyLogic. В ходе исследования группе китайских медиков удалось рассчитать некоторые усредненные показатели, в частности частоту заражения 2019-nCoV при личном контакте у пациентов (10,4%); продолжительность инкубационного периода (≈6,6 дней) и время, которое необходимо, чтобы излечиться при назначенном курсе лечения (≈9,8 дней).

К сожалению, стоит признать, что на сегодняшний день не существует эффективной и универсальной модели, которая на основе базовой статистики заболеваний смогла бы достаточно точно спрогнозировать возникновение и оценить протекание того или иного заболевания. Каждая болезнь имеет свои особенности (этиологию) с одной стороны, а кроме того, даже в рамках одной эпидемии эти особенности в разных социумах могут проявляться неодинаково, что мы можем наблюдать на примере последней пандемии коронавирусной инфекции COVID-19, вызванной коронавирусом SARS-CoV-2. Особенно это хорошо прослеживается на фоне сравнения течения заболевания в Юго-Восточной Азии и в странах Южной и Центральной Европы, Латинской Америки. Однако современное моделирование (особенно в сочетании разных методов – математических и имитационных) позволяет оценить масштабы и последствия эпидемий при различных сценариях и действиях властей, что должно повысить качество и эффективность предпринимаемых мер и управленческих решений.

Автор статьи – Иванов М.В., начальник отдела аналитических и социологических исследований МАУ «ИРСИ»

Источник

Зараза, гостья наша

Как математика помогает бороться с эпидемиями

Эпидемии издавна угрожали человечеству, и только в ХХ веке были разработаны эффективные средства борьбы с инфекциями. К числу этих средств принадлежат и системы дифференциальных уравнений — математика помогает моделировать распространение эпидемий и помогает понять, как следует с ними бороться. Это наш третий материал о самых интересных дифференциальных уравнениях и о том, где и как они применяются (предыдущие материалы можно прочитать здесь и здесь). Если вы читаете нас с телефона, переключайте страницу на десктопную версию, так вы сможете увидеть интерактивный график целиком.

В XXI веке мир уже успел столкнуться с эпидемией птичьего гриппа в Юго-Восточной Азии (в 2013 году) и вспышкой заболеваний лихорадкой Эбола в Африке (2015). Но в истории человечества бывали и куда более масштабные эпидемии.

В результате Первой мировой войны, вызвавшей перемещение большого количества людей, в 1918 году распространился испанский грипп, охвативший более 500 миллионов человек и погубивший каждого десятого заболевшего. Эта пандемия стала самой масштабной за всю историю человеческой цивилизации, коснувшись до 30 процентов населения Земли.

В медицинской классификации эпидемией называют прогрессирующее распространение инфекционного заболевания на уровне выше среднего на данной территории. В случае распространения эпидемии на большие территории или территории многих стран говорят о пандемии.

Для эпидемии среди животных применяется термин эпизоотия, а среди растений — эпифития. Этим явлениям ученые также уделяют большое внимание, поскольку они, в свою очередь, помогают понять механизм распространения инфекций.

Изучение механизмов развития и распространения эпидемий является важным способом борьбы с заболеваниями наряду с поиском новых лекарств, вакцинацией и профилактическими мерами. На помощь медикам пришли математики — для этого им пришлось объединить дифференциальные уравнения и теорию вероятности.

Первую попытку использовать математический аппарат для исследования механизмов распространения заболеваний предпринял Даниил Бернулли, ранее открывший первые законы гидродинамики. Следующий шаг сделал Уильям Фарр, применивший в 1840 году нормальное распределение к анализу смертности от оспы.

Наконец, опираясь на работы большого числа предшественников, британские ученые Андерсон Кермак и Уильям Маккендрик разработали широко применяемую сегодня модель SIR. Эта аббревиатура происходит от английских слов Susceptible — Infected — Recovered, буквально означающих «восприимчивые — инфицированные — выздоровевшие». Под «восприимчивыми» тут подразумеваются еще не инфицированные организмы.

В рамках этой модели с помощью систем дифференциальных уравнений (при условии непрерывности времени и большой популяции) или разностных уравнений (при дискретном времени и ограниченной популяции) описывается динамика распространения заболевания.

Модель SIR

SIR–модель получила заслуженную популярность в силу простоты построения и использования. Ее применение позволяет точно моделировать эпидемии гриппа и других заболеваний в больших городах, вводить новые параметры и анализировать разные сценарии.

Система уравнений SIR:

Первое уравнение системы означает, что изменение числа здоровых (и при этом восприимчивых к заболеванию) индивидуумов уменьшается со временем пропорционально числу контактов с инфицированными. После контакта происходит заражение, восприимчивый переходит в состояние инфицированного.

Второе уравнение показывает, что скорость увеличения числа заразившихся растет пропорционально числу контактов здоровых и инфицированных и уменьшается по мере выздоровления последних.

Третье уравнение демонстрирует, что число выздоровевших в единицу времени пропорционально числу инфицированных. Иначе говоря, каждый заболевший через некоторое время должен поправиться.

Таким образом, мы видим, что заболевание в модели SIR развивается по схеме «восприимчивые становятся инфицированными, потом выздоравливают». Условие

описывает неизменность численности популяции (и не учитывает случаи смерти от заболевания).

Графики решения выглядят так (это интерактивный график, в нем можно регулировать параметры β и γ):

Здесь синяя линия — число восприимчивых индивидов, красная — инфицированных, зеленая — переболевших.

Красный график интенсивности эпидемии, показывающей количество одномоментно болеющих индивидов, определяется параметром:

Эта величина получила название «базовый коэффициент воспроизведения».

В 2012 году британская компания Ndemic Creation выпустила игру “Plague Inc.”, биологический симулятор эпидемий. По сценарию игры необходимо развить одно из выбранных заболеваний настолько, чтобы оно уничтожило жизнь на Земле.

На базовых уровнях игры распространение заболевания происходит в точном соответствии с моделью SIR. Если принять, что вместо выздоровления происходит гибель организма, то зеленый график становится графиком числа умерших — каждый игрок может увидеть его при успешном прохождении уровня.

“Plague Inc.” является одной из лучших стратегий среди существующих на рынке и на протяжении многих лет пользуется популярностью у десятков миллионов поклонников.

SIR-модель перестает работать в случае необходимости учитывать неоднородность популяции (например, различную плотность населения в разных районах), разные пути передачи инфекции и факторы случайности, значимые в малых популяциях и на начальной фазе распространения заболевания.

Развитием модели SIR стали, в частности, следующие модели:

Модель SEIR

Именно по этой модели развиваются по-настоящему опасные эпидемии, поскольку длительный инкубационный период может препятствовать своевременному обнаружению заболевания. В этом случае есть риск, что заболевание охватит значительное число индивидуумов в популяции.

Инфекция развивается по схеме «восприимчивые» — «контактные» — «инфицированные» — «выздоровевшие» и описывается системой уравнений:

Как и в модели SIR, первое уравнение системы означает, что изменение числа здоровых (и при этом восприимчивых к заболеванию) индивидуумов уменьшается со временем пропорционально числу контактов с инфицированными. После заражения здоровый индивид переходит в состояние контактного по данному заболеванию, или носителя инфекции.

Второе уравнение вносит задержку по времени при переходе из состояния контактного в состояние инфицированного (больного). Это происходит через время, равное инкубационному периоду болезни.

Третье уравнение описывает переход из состояния «контактный» в состояние «инфицированный».

Четвертое уравнение демонстрирует, что число выздоровевших в единицу времени пропорционально числу инфицированных. При этом в каждом состоянии индивидуум может погибнуть, что учитывает коэффициент μ в каждом уравнении.

Иначе говоря, в каждый момент времени каждый индивидуум с определенной вероятностью может заразиться, через некоторое время — заболеть, а затем поправиться либо погибнуть.

Численность популяции N = S + E + I + R при этом не является постоянной с течением времени.

Интенсивность эпидемии описывает базовый коэффициент воспроизведения:

49 из 100

Желающие воочию увидеть, как «работают» модели распространения эпидемии, могут сделать это с помощью симулятора, созданного канадским исследователем Беном Бэбкуком.

Например, построим симуляцию, использовав следующие параметры:

С помощью моделирования мы видим, что 49 организмов из 100 погибнут в результате эпидемии длительностью в 29 дней.

Симуляция эпидемии с заданными параметрами

Epidemic Simulator позволяет моделировать результаты эпидемий при различных плотности популяции, заразности, летальности и устойчивости заболеваний.

Модель SIS

Модель «восприимчивые — инфицированные — восприимчивые» применима при анализе распространения заболеваний, к которым не вырабатывается иммунитет, например гриппа и ОРВИ. Она описывается следующей системой уравнений:

Вместе первое и второе уравнение означают, что число здоровых и больных в сумме не меняется, а число заражений пропорционально числу контактов здоровых и больных.

Второе уравнение описывает изменение числа заболевших в единицу времени, которое пропорционально числу заражений (числу контактов здоровых и инфицированных индивидуумов) за вычетом числа выздоровлений.

График развития заболевания в соответствии с этой моделью выглядит так (график интерактивный, можно регулировать параметры β и γ):

Синяя линия — число восприимчивых индивидов, красная — инфицированных в текущий момент.

Модель MSEIR

Эта модель, построенная для заболевания с инкубационным периодом и учитывающая иммунитет детей, приобретенный внутриутробно, — одна из самых сложных для анализа в силу наличия большого числа независимых параметров. Система уравнений для нее выглядит так:

Источник