какой метод называется методом перемещений
Метод перемещений
Метод перемещений – метод расчета, в котором в качестве неизвестных принимают перемещения в дополнительно введенных избыточных связях.
[Полякова, Т.Ю. Автодорожные мосты: учебный англо-русский и русско- английский терминологический словарь-минимум / Т.Ю. Полякова, Н.Г. Карасева, Д.В. Поляков. – М.: МАДИ, 2015. – 120 с.]
Полезное
Смотреть что такое «Метод перемещений» в других словарях:
метод перемещений — Метод строительной механики для определения усилий и перемещений в статически неопределимых конструктивных системах, при котором в качестве основных неизвестных выбираются линейные и угловые перемещения [Терминологический словарь по строительству … Справочник технического переводчика
МЕТОД ПЕРЕМЕЩЕНИЙ — метод строительной механики для определения усилий и перемещений в статически неопределимых конструктивных системах, при котором в качестве основных неизвестных выбираются линейные и угловые перемещения (Болгарский язык; Български) метод на… … Строительный словарь
метод муара — метод муаровых полос Эксперим. теоретич. м. определения деформаций и перемещений по чередующимся светлым и темным полосам, образующ. вследствие механич. интерференции, возник, при наложении двух или более систем линий, сеток, растров или точек. М … Справочник технического переводчика
МЕТОД — (от греч. methodos путь, способ исследования, обучения, изложения) совокупность приемов и операций познания и практической деятельности; способ достижения определенных результатов в познании и практике. Применение того или иного М. определяется… … Философская энциклопедия
Метод сил — – метод строительной механики для определения усилий и перемещений в статически неопределимых системах, при котором в качестве основных неизвестных выбирают силы, заменяющие воздействия лишних связей. [Терминологический словарь по… … Энциклопедия терминов, определений и пояснений строительных материалов
МЕТОД СИЛ — метод строительной механики для определения усилий и перемещений в статически неопределимых системах, при котором в качестве основных неизвестных выбирают силы, заменяющие воздействия лишних связей (Болгарский язык; Български) метод на сидите… … Строительный словарь
МЕТОД КИНЕМАТИЧЕСКИЙ — метод определения усилий в плоской или пространственной системе от неподвижной или подвижной нагрузки, предполагающий освобождение системы от некоторой кинематической связи и рассмотрение в образованной таким образом системе виртуальных… … Строительный словарь
метод кинематический — Метод определения усилий в плоской или пространственной системе от неподвижной или подвижной нагрузки, предполагающий освобождение системы от некоторой кинематической связи и рассмотрение в образованной таким образом системе виртуальных… … Справочник технического переводчика
метод пространственного кодирования — Метод, основанный на предварительном преобразовании значений непрерывной измеряемой величины в пропорциональные им пространственные перемещения с последующим преобразованием этих пространственных перемещений в цифровой код. [ГОСТ 13607 68]… … Справочник технического переводчика
метод сил — Метод строительной механики для определения усилий и перемещений в статически неопределимых системах, при котором в качестве основных неизвестных выбирают силы, заменяющие воздействия лишних связей [Терминологический словарь по строительству на… … Справочник технического переводчика
РАСЧЕТ СТАТИЧЕСКИ НЕОПРЕДЕЛИМЫХ СИСТЕМ МЕТОДОМ ПЕРЕМЕЩЕНИЙ
Как уже знаем, при расчете статически неопределимых систем методом сил исключаются лишние связи, а за неизвестные принимаются силы (усилия) в этих связях. После их вычисления из канонических уравнений можно определять все остальные усилия, а также перемещения, напряжения и деформации системы.
Напряженно-деформированное состояние (НДС) статически неопределимых систем можно устанавливать и по-другому. В этом случае связи не исключаются, а делается наоборот – в систему вводятся дополнительные связи. Тогда за неизвестные принимаются перемещения во введенных связях, которые определяются из канонических уравнений. Поэтому этот метод называется методом перемещений.
Неизвестные метода перемещений
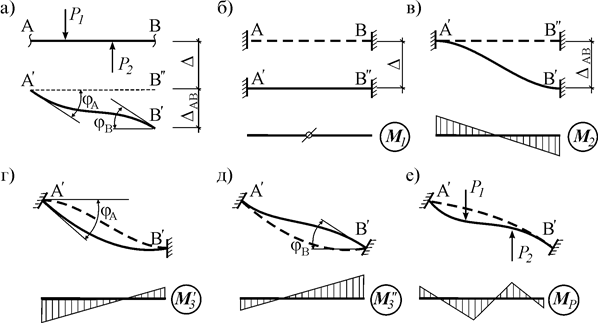
Установим минимальное число узловых перемещений, необходимых для определения напряженно-деформированного состояния статически неопределимой стержневой системы.
С этой целью определим простейшие деформации некоторого стержня АВ стержневой системы, которые он получает при переходе в новое положение 
под воздействием внешней нагрузки (рис. (10.1 а). Данная задача упрощается, если стержень закрепить по обоим концам и, задавая его концам некоторые независимые перемещения, привести стержень к окончательному деформированному состоянию .
Как следует из рисунков, для этого концам закрепленного стержня АВ необходимо последовательно задавать поступательные (линейные) перемещения 
и 
(рис. 10.1 б, в), угловые перемещения 
и 
(рис. 10.1 г, д), а внутри стержня приложить внешнюю нагрузку (рис. 10.1 е).
При этом от поступательного перемещения 
всего стержня внутренние усилия и деформации не возникают (на рис. 10.1 б 
). Внутренние усилия и деформации от местной нагрузки, действующей в пределах закрепленного стержня АВ, можно найти отдельно. Значит, для определения НДС всего стержня достаточно знать три неизвестных перемещения – два угловых перемещения его концов , и одно поступательное перемещение – взаимное смещение концов стержня 
. Поэтому степень кинематической неопределимости такого стержня равняется трем.
Выбор основной системы
Основная система метода перемещений должна быть кинематически определимой. Значит, для ее получения в заданную систему следует ввести столько дополнительных связей, чтобы концы всех стержней были закреплены и исключены их перемещения. Поэтому общее число вводимых связей будет равно числу неизвестных метода перемещений.
Однако число вводимых связей (а значит и число неизвестных метода перемещений) может быть весьма большим. Например, рама на рис. 10.2 а состоит из пяти стержней. По результатам проведенного выше анализа, степень ее кинематической неопределимости (или число неизвестных метода перемещений) будет 5·3=15.
Это число можно уменьшить, если принять следующие гипотезы:
1) поперечные и продольные деформации стержней малы;
2) длина хорды, соединяющей концы изогнутого стержня, равна первоначальной длине стержня;
3) в упругом рамном узле углы между стержнями сохраняются.
Действительно, в этом случае в данной раме достаточно будет знать только три перемещения – поступательное перемещение и два угловых перемещения 
и 
(рис. 10.2 а). Таким образом, число неизвестных уменьшилось намного – с пятнадцати до трех.
Из третьей гипотезы следует, что число неизвестных угловых перемещений будет определяться по формуле
= числу упругих рамных узлов.
Для определения числа неизвестных поступательных перемещений (в дальнейшем их будем называть линейными перемещениями) во все узлы рамы, включая и опоры, нужно ввести шарниры (рис. 10.2 б). Тогда число линейных перемещений будет легко определяться по известной формуле кинематического анализа для фермы
.
В рассматриваемой раме имеем 
=2× 6 – 5 – 6 =1.
Общее число всех неизвестных перемещений определяется по формуле
= +
После определения числа неизвестных в ЗС следует вводить столько же связей для исключения перемещений концов ее стержней. Например, в рассмотренную раму введем две заделки и одну опорную связь. Полученная схема (рис. 10.2 в) будет основной системой (ОС) метода перемещений.
Таким образом, для получения ОС метода перемещений необходимо:
– в упругие рамные узлы заданной системы ввести заделок;
– в направлении поступательных перемещений узлов заданной системы ввести опорных связей (они вводятся так, чтобы система с введенными шарнирами стала геометрически неизменяемой).
Введенные связи, хотя внешне и похожи на обычные опорные связи, от них принципиально отличаются, потому что: 1) введенная заделка исключает лишь угловое перемещение узла, оставляя возможность линейного смещения; 2) введенная опорная связь исключает только линейное перемещение узла, оставляя возможность поворота (рис. 10.2 г, д).
При соблюдении этих требований ОС метода перемещений будет единственной.
Пусть необходимо выбрать ОС метода перемещений для рамы (рис. 10.3 а). Она имеет четыре жестких узла. Значит, число угловых неизвестных =4. Для определения числа линейных неизвестных во все узлы и опоры рамы введем шарниры (рис. 10.3 б). Тогда имеем: 
. Поэтому общее число неизвестных будет 
+ =4+2=6. Вводя в жесткие узлы ЗС четыре заделки и две опоры, исключающие линейные перемещения узлов рамы (последние вводятся так, чтобы механизм на рис. 10.3 б стал геометрически неизменяемым), получаем требуемую ОС (рис. 10.3 в).
Сущность метода перемещений
Данный вопрос изучим на следующем примере (рис. 10.4 а). Эта рама четырежды статически неопределима. При ее расчете методом сил нужно исключать четыре лишние связи и выбирать основную систему, например, такую как на рис. 10.4 б.
При использовании же метода перемещений раму следует превратить в кинематически определимую. Для этого в ЗС достаточно ввести + =1+0=1 кинематическую связь. Если неизвестное угловое перемещение узла обозначить через Z, получим ОС показанную на рис. 10.4 в.
Потребуем, чтобы усилия и деформации ОС были такими же как у ЗС. Для этого перемещение Z должно быть равно углу поворота узла рамы j (рис. 10.4 а), а реактивный момент во введенной заделке основной системы (рис. 10.4 в) должен равняться нулю:
Эту реакцию определим, рассматривая единичное и грузовое состояния основной системы.
В единичном состоянии введенной связи зададим единичное перемещение Z=1 и определим возникающую в ней реакцию r (рис. 10.4 г). Такая реакция от единичного перемещения называется жесткостью.
В грузовом состоянии приложим только внешнюю нагрузку и во введенной связи основной системы определим реакцию RP (рис. 10.4 д).
С учетом упругости системы и принципа суперпозиции наше уравнение приводится к виду
Оно называется каноническим уравнением метода перемещений. Если известны реакции r и RP, то из него можно найти величину узлового перемещения:
Если степень кинематической неопределимости стержневой системы равна n, ее ОС получается введением n дополнительных связей с неизвестными Z1, Z2, …, Zn. Чтобы ОС была эквивалентна ЗС, реакции во введенных связях должны равняться нулю. С учетом этого можно записать n уравнений. После рассмотрения n единичных состояний, одного грузового состояния и дальнейшего определения реакций (реактивных усилий) во всех состояниях, эти уравнения приводятся к следующему виду:
Все вместе они называются системой канонических уравнений метода перемещений. Здесь 
– главные коэффициенты, 
– боковые коэффициенты. Свободные члены 
являются грузовыми коэффициентами.
После введения матриц и векторов
r= 
, Z = 
,RP = 
,0 = 
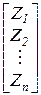
система канонических уравнений записывается в матричной форме: r · Z + RP = 0,
где r – матрица жесткости, Z – вектор неизвестных, RP – вектор нагрузки, 0 – нуль-вектор. Отсюда определяется вектор неизвестных:
Z = – r –1 RP,
где r – 1 – обратная матрица жесткости.
В о п р о с ы
1. Какие величины являются неизвестными метода перемещений?
2. Что такое степень кинематической неопределимости?
3. Какие гипотезы принимаются при расчете рам методом перемещений?
4. Как определяется основная система метода перемещений?
5. Что называется жесткостью?
6. В чем заключается сущность метода перемещений?
7. Как записывается система канонических уравнений метода перемещений?
3. Основная система метода перемещений
Основная система метода перемещений получается не отбрасыванием лишних связей, как это делается в методе сил, а наоборот, введением дополнительных (фиктивных) связей, закрепляющих узлы от их возможных угловых и линейных смещений, которые были выявлены ранее (при определении степени кинематической неопределимости n); то есть во все жесткие узлы, которые могут поворачиваться, устанавливаются дополнительные (фиктивные) жесткие заделки, закрепляющие их от поворота, а все узлы (жесткие и шарнирные, которые могут линейно смещаться (nл), закрепляются от этих смещений с помощью постановки дополнительных (фиктивных) линейных связей. В качестве неизвестных при этом принимаются перемещения этих дополнительных связей (вместе, конечно, с узлами) и обозначаются они Zi (i =1. n). Следует отметить, что дополнительная (фиктивная) заделка в отличие от действительной заделки имеет только одну связь от поворота, то есть она не закрепляет от линейных смещений.
Д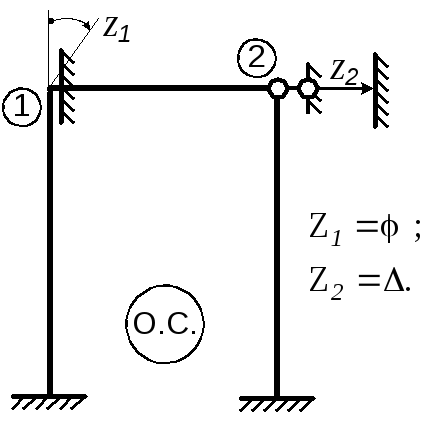
ля рамы, представленной на рис. 1а, основная система (О.С.) метода перемещений имеет вид, изображенный на рис. 5. Анализ этой О.С. показывает,
что узел 1 с учетом установленных дополнительных связей и используемых допущений (раздел 1) будет вести себя так, будто в нем стоит полная действительная заделка, через которую никакие перемещения не передаются; аналогично узел 2 в О.С. имеет, по существу, шарнирно-неподвижную опору и через него никакие перемещения тоже передаваться не
!Таким образом, анализ показывает, что О.С. метода перемещений является статически неопределимой и, по существу, представляет собой совокупность отдельных независящих друг от друга однопролетных балочек с одним либо двумя защемленными концами вида:
или
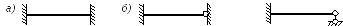
При этом изгибающие моменты в О.С. метода перемещений возникают только в тех балочках (только на тех участках), которые непосредственно подвержены какому-либо воздействию. На остальных же участках изгибающие моменты возникать не будут.
Для рамы на рис. 3а основная система (О.С.) метода перемещений представлена рис. 3б.
4. Канонические уравнения метода перемещений
Таким образом, расчет статически неопределимой системы методом перемещений выполняется с использованием основной системы этого метода, которая должна работать также как исходная система. Для достижения этого на основную систему метода перемещений накладываются соответствующие условия, в качестве которых принимается равенство нулю реакций в дополнительных связях от совместного действия всех неизвестных перемещений и внешних нагрузок, так как в заданной системе этих дополнительных связей нет и, следовательно, реакций в них тем более быть не может. Таким образом, ставится задача подобрать такие значения неизвестных перемещений, при которых от заданных нагрузок реактивные усилия в дополнительных связях должны быть равны нулю, так как этих дополнительных связей в исходной (рассчитываемой) системе нет.
Указанные условия записывают в виде, так называемых, канонических уравнений метода перемещений:
Rip реактивное усилие (момент, сила) в i-той дополнительной связи (заделке, линейной связи) от действия внешней нагрузки.
Приведем примеры физического смысла коэффициентов канонических уравнений и уравнений в целом, например, для основной системы метода перемещений, представленной на рис. 3:
r11 реактивный момент в 1-ой дополнительной заделке от ее же поворота на единичный угол;
r53 реактивная сила в 5-ой фиктивной линейной связи от поворота 3-ей фиктивной заделки на угол равный единице;
r26 реактивный момент во 2-ой дополнительной заделке от единичного линейного смещения 6-ой дополнительной линейной связи;
R4p реактивная сила в 4-ой фиктивной линейной связи от действия внешней нагрузки;
3. Основная система метода перемещений
Основная система метода перемещений получается не отбрасыванием лишних связей, как это делается в методе сил, а наоборот, введением дополнительных (фиктивных) связей, закрепляющих узлы от их возможных угловых и линейных смещений, которые были выявлены ранее (при определении степени кинематической неопределимости n); то есть во все жесткие узлы, которые могут поворачиваться, устанавливаются дополнительные (фиктивные) жесткие заделки, закрепляющие их от поворота, а все узлы (жесткие и шарнирные, которые могут линейно смещаться (nл), закрепляются от этих смещений с помощью постановки дополнительных (фиктивных) линейных связей. В качестве неизвестных при этом принимаются перемещения этих дополнительных связей (вместе, конечно, с узлами) и обозначаются они Zi (i =1. n). Следует отметить, что дополнительная (фиктивная) заделка в отличие от действительной заделки имеет только одну связь от поворота, то есть она не закрепляет от линейных смещений.
Для рамы, представленной на рис. 1а, основная система (О.С.) метода перемещений имеет вид, изображенный на рис. 5. Анализ этой О.С. показывает,
что узел 1 с учетом установленных дополнительных связей и используемых допущений (раздел 1) будет вести себя так, будто в нем стоит полная действительная заделка, через которую никакие перемещения не передаются; аналогично узел 2 в О.С. имеет, по существу, шарнирно-неподвижную опору и через него никакие перемещения тоже передаваться не
!Таким образом, анализ показывает, что О.С. метода перемещений является статически неопределимой и, по существу, представляет собой совокупность отдельных независящих друг от друга однопролетных балочек с одним либо двумя защемленными концами вида:
или
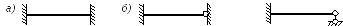
При этом изгибающие моменты в О.С. метода перемещений возникают только в тех балочках (только на тех участках), которые непосредственно подвержены какому-либо воздействию. На остальных же участках изгибающие моменты возникать не будут.
Для рамы на рис. 3а основная система (О.С.) метода перемещений представлена рис. 3б.
4. Канонические уравнения метода перемещений
Таким образом, расчет статически неопределимой системы методом перемещений выполняется с использованием основной системы этого метода, которая должна работать также как исходная система. Для достижения этого на основную систему метода перемещений накладываются соответствующие условия, в качестве которых принимается равенство нулю реакций в дополнительных связях от совместного действия всех неизвестных перемещений и внешних нагрузок, так как в заданной системе этих дополнительных связей нет и, следовательно, реакций в них тем более быть не может. Таким образом, ставится задача подобрать такие значения неизвестных перемещений, при которых от заданных нагрузок реактивные усилия в дополнительных связях должны быть равны нулю, так как этих дополнительных связей в исходной (рассчитываемой) системе нет.
Указанные условия записывают в виде, так называемых, канонических уравнений метода перемещений:
Rip реактивное усилие (момент, сила) в i-той дополнительной связи (заделке, линейной связи) от действия внешней нагрузки.
Приведем примеры физического смысла коэффициентов канонических уравнений и уравнений в целом, например, для основной системы метода перемещений, представленной на рис. 3:
r11 реактивный момент в 1-ой дополнительной заделке от ее же поворота на единичный угол;
r53 реактивная сила в 5-ой фиктивной линейной связи от поворота 3-ей фиктивной заделки на угол равный единице;
r26 реактивный момент во 2-ой дополнительной заделке от единичного линейного смещения 6-ой дополнительной линейной связи;
R4p реактивная сила в 4-ой фиктивной линейной связи от действия внешней нагрузки;