какой метод изначально применялся для обучения навыкам решения сложных экономических задач ответ
Нестандартные решения сложных задач
Меня интересуют различные методы системного и творческого мышления, которое можно использовать в реальной жизни для решения сложных задач. О нескольких методах расскажу в данной статье.
Недавно прочитал книгу Торп С. — Учебник креативного мышления. Простой подход к нестандартным решениям – 2010. В ней предлагается интересный подход для развития навыков решения сложных задач.
Основная мысль автора – чтобы решать сложные задачи, нужно сворачивать с колеи шаблонного мышления, нарушать правила, которые зачастую нам не дают взглянуть на проблему шире. Вот что пишет автор:
Неспособность разрешить какую-то проблему вполне может объясняться тем, что вы застряли в «колее» правил. Мы все живем по правилам — укоренившимся в нас шаблонам мышления, которые ошибочно принимаем за истину. Наши правила формируются естественным образом в результате многократного использования одних и тех же идей. Следуя правилам, мы постепенно увязаем в глубокой «колее», и тогда любые неординарные идеи остаются вне нашего поля зрения.
Как нарушать правила, отлично показано на примере игры «Крестики-нолики».
Многие неразрешимые проблем похожи на игру в «крестики-нолики»» Выигрыш кажется невозможным, как бы ты не играл. Однако нарушив (или расширив) правила можно получить победу множеством путей.
Ход вне очереди
В «крестики-нолики» выиграть очень просто, если делать ходы вне очереди! Конечно в контексте крестиков-ноликов, нарушение правил – это обман. Однако речь идет не о моральных принципах, а о правилах, которые предписывают нам, как следует решать проблему.
Если правила не работают, то почему бы не сыграть на опережение, делая дополнительные ходы.
Мало кому приходит в голову сделать ход вне очереди в реальном мире, но, в сущности, этот прием используется с незапамятных времен. Например, после одного из сражений гражданской войны в Америке генерал Роберт Ли объявил своим офицерам, что генерал Грант двинется на Спотсильванию, так как это наилучшее для него решение. Ли разработал кратчайший маршрут к этому пункту и приказал войскам двигаться туда. Войска Ли сделали, так сказать, ход вне очереди и прибыли в Спотсильванию прежде, чем туда смогла добраться армия Гранта.
Ходы вне очереди — распространенное явление в мире бизнеса. Когда изготовители Тайленола узнали, что аналогичное обезболивающее средство Датрил будет продаваться со значительной скидкой, они сделали ход вне очереди. Они установили цену ниже стоимости Датрила еще до того, как изготовители последнего смогли объявить о своей цене. Рекламная кампания нового лекарства провалилась, и Тайленол удержал свои позиции на рынке.
Мы в компании, часто играем на опережение – ещё на предварительном изучении объекта автоматизации разрабатываем прототип системы. Такой подход нам позволяет глубже понять, что нужно сделать, а заказчику увидеть серьёзность наших намерений.
Используйте активы соперника
Выстроить в ряд три значка совсем не трудно, если к своим двум ноликам прибавить чужой крестик. Зачем ограничивать себя собственными ресурсами? )
Адмирал военно-морского флота США Гарри Ярнелл был первым, кто разработал план нападения японцев на Перл-Харбор. Он определил наиболее перспективные направления и стратегию атаки. В 1932 году он даже провел показательные учения с участием двух авианосцев США. Императорский военно-морской флот Японии превратил план американского адмирала в собственную успешную атаку на базу ВМС США. Японцы не постеснялись воспользоваться американским планом сражения. Если план эффективен, осознано используйте его, независимо от источника.
В шашках и шахматах победная комбинация основывается на расположении, как своих фигур, так и противника, причем именно использование фигур противник зачастую является ключевым элементом победного плана.
В бизнесе предприниматели часто изучают что сдали конкуренты, учитывают их ошибки и создают более прибыльную систему.
Проявите гибкость (и правильно ставьте задачи)
Вы сможете выиграть в «крестики-нолики» или разрешить другие сложные задачи, если примените гибкое определение термина «победа». Позвольте вашему ряду изогнуться, и победа у вас в кармане. Иногда определенные нами условия победы слишком строги или не соответствуют характеру сложившейся ситуации. Измените определение успеха и решение станет возможным.
Кроме того, если задача была поставлена неправильно, то возможно никому не под силу её решить. Задача должна ставиться конструктивно, в расчете на нетривиальные решения, отличные от ваших первоначальных ожиданий. Деструктивная постановка задач связана с таким количеством условий и ограничений, что достижение цели оказывается за пределами человеческих возможностей. Примером деструктивной постановки задачи может быть желание «летать, махая руками, словно крыльями».
При конструктивной постановке задачи приемлемым будет любое решение, позволяющее вам «оторваться от земли». Правильная постановка задачи расширяет диапазон возможных решений.
Сотрудничайте
Правило, ведущее к обязательному проигрышу одной стороны, может оказаться самым большим препятствием на пути к победе любого из участников игры. Сотрудничество с соперником может обеспечить выигрыш вам обоим.
Однажды я услышал фразу на всегда запавшую мне в душу: «В одного можно вырастить только супер-картошку!!». Имеется ввиду, что для решения действительно сложных задач нужна команда и желание сотрудничать.
Пробуйте решать сложные проблемы – нарушайте правила!
Обучение решению экономических задач в школьном курсе математики
Вид работы: Проект
Тема: Обучение решению экономических задач в школьном курсе математики
Содержание
Глава 1. Теоретические основы обучению решения экономических задач в школьном курсе математики. 5
1.1. Межпредметные связи математики и экономики. 5
1.2. Понятие и история возникновения процента, экономической и финансовой задачи, а также основные экономические функции. 7
1.3. Классификация экономических задач по ЕГЭ.. 13
1.4. Вывод по 1 главе. 17
Глава 2. Методические аспекты обучению решению экономических задач в школьном курсе математики. 18
2.1 Анализ школьных учебников, КИМ, ЕГЭ, ОГЭ на наличие и типы.. 18
2.2. Методы решения экономческих задач. 21
2.3 Разработка элективного курсы к подготовке по решению экономических задач. 29
2.4 Вывод по главе 2. 41
Список использованной литературы.. 45
ВВЕДЕНИЕ
Актуальность. Обучение решению экономических задач в школьном курсе математики сегодня весьма актуально как для успешной сдачи Единого Государственного Экзамена – ЕГЭ, так и в посведневной жизни.
ЕГЭ по математике содержит задачи экономического содержания на проценты, которые решаются с помощью простых и сложных процентов. Проанализировав сборники заданий по подготовке к ЕГЭ, следует вывод, что необходимо в совершенстве научиться решать задачи на проценты, чтобы сдать ЕГЭ по математике на максимально допустимый балл.
Также современная жизнь делает навык решения экономических задач актуальным, так как сфера практического приложения расширяется. Вопросы инфляции, повышения цен, снижения покупательской способности, платежей, налогов, прибыли, кредиты, начисление зарплаты, депозитные счета в Сбербанке касаются каждого человека в нашем общества. Планирование семейного бюджета невозможны без умения производить несложные финансовые вычисления.
Объект исследования – обучение решению экономических задач в школьном курсе математики.
Цель: обобщение, углубление и систематизация знаний по теме «Обучение решению экономических задач в школьном курсе математики», решение экономических задач по заданиям ЕГЭ.
Для решения данной цели я поставила перед собой ряд задач:
Материалы: пособия по подготовке к ЕГЭ.
Методы исследования – поиск необходимой информации в сети Интернет, теоретический анализ и синтез научной и учебной литературы, сравнение, систематизация информации, обобщение вывод, подбор и решение задач.
Информационной базой исследования послужили нормативные и законодательные акты Российской Федерации, труды отечественных учёных по данной тематике, научные публикации, материалы периодических изданий.
Курсовая работа состоит из введения, двух глав, заключения, списка использованной литературы и приложений.
ГЛАВА 1. Теоретические основы обучению решению экономических задач в школьном курсе математики
Широко известно, что экономическая образованность и мышление обучающихся формируются не только при изучении курса экономики, но не в меньшей степени — на основе всего комплекса изучаемых дисциплин. В общей задаче насыщения дисциплин экономическим содержанием математике принадлежит особая роль. Это объясняется тем, что многие экономические проблемы поддаются анализу с помощью математического аппарата. Взаимодействие математики и экономики приносит обоюдную пользу: математика получает широчайшее поле для многообразных приложений, а экономика — могучий инструмент для получения новых знаний.
В современных образовательных учреждениях среднего профессионального уровня экономика преподается достаточно длительное время. При этом сразу же были обнаружены пробелы в школьных курсах математики, полностью игнорирующие многие элементарные, но очень важные для повседневной жизни, приемы анализа экономических процессов. Обучающиеся плохо понимали экономические графики, не ориентировались в том, как провести хотя бы самый простой анализ динамических, т.е. развивающихся во времени, процессов[22].
Для того чтобы познакомить обучающихся с азами коммерческой математики, необходимыми не только профессиональным экономистам, но и каждому человеку, очень важно работать над проблемой активизации познавательной деятельности обучающихся через межпредметную связь экономики и математики.
— выделять математические модели, функции, системы уравнений и неравенств, используемые в экономике и показать их практическое применение;
— повышать познавательный интерес к учебной деятельности обучающихся;
— разрабатывать систему уроков по математике с экономической направленностью;
— отслеживать результаты обученности, межпредметных умений и навыков обучающихся[3].
Объединение разрозненных частей знаний на уроке, известное как процесс установления межпредметных связей – только часть устойчивого стремления всего живого к целостности. Обращение к интеграции в широком смысле слова, как средству создания целостного восприятия учебного материала, объясняется рядом преимуществ этого достаточно нового вида образовательной деятельности на уроке, главными из которых являются:
— Мир, окружающий обучающихся, познается ими в своем многообразии и единстве.
— Межпредметные связи развивают потенциал самих обучающихся, побуждают к активному познанию окружающей действительности, к осмыслению и нахождению причинно-следственных связей, к развитию логики, мышления, коммуникативных способностей.
— Форма проведения уроков нестандартна, интересна. Использование различных видов работы в течение занятия поддерживает внимание обучающихся на высоком уровне, что позволяет говорить о достаточной эффективности уроков.
Такие занятия снимают утомляемость, перенапряжение обучающихся за счет переключения на разнообразные виды деятельности, резко повышают познавательный интерес, служат развитию у обучающихся внимания, мышления, речи и памяти.
— За счет усиления межпредметных связей высвобождаются учебные часы, которые можно использовать для дополнительных уроков практической направленности.
— Интеграция дает возможность для самореализации, самовыражения, творчества преподавателя и обучающихся, способствует раскрытию скрытых способностей[31].
Таким образом, работа в данном направлении положительно отражается на интеллектуальном развитии обучающихся, их воспитании, на формирование профессионально значимых качеств личности. Развиваются и общеучебные и надучебные навыки: анализ, синтез, сравнение, умение работать с научно – учебной и дополнительной литературой и т.п. умения, что еще раз подтверждает целесообразность использования экономических понятий и методов в математике.
1.2 Понятие и история возникновения процента, экономической и финансовой задачи, а также основные экономические функции
Экономические задачи – это задачи, решаемые в процессе экономического анализа, планирования, проектирования, связанные с определением искомых неизвестных величин на основе исходных данных. В отличие от математических, экономические задачи не всегда удается формализовать, свести только к расчету. Их решение сопровождается поиском недостающих данных, экспертными оценками, обсуждением, принятием решений.
История возникновения процентов.
Процент — имеет латинское происхождение: «pro centum» — это «на сто». Процентом называется сотая часть числа.
Проценты были известны в Индии ещё в V в. С давних пор счет велся в десятичной системе счисления. Также проценты были распространены в Древнем Риме. Римляне называли процентами деньги, которые платил должник заимодавцу за каждую сотню. Они брали с должника лихву (т. е. деньги сверх того, что дали в долг). От римлян проценты перешли к другим народам в Европе[29].
В средние века в Европе в связи с развитием торговли особо обращали внимание на умение вычислять проценты. Впервые опубликовал таблицы для расчета процентов Симон Стевин – инженер из города Брюгге (Нидерланды). Это произошло в 1584 году.
Употребление термина «процент» в России начинается в конце XVIII в. Долгое время под процентами понималось исключительно прибыль или убыток на каждые 100 рублей. Проценты применялись только в торговых и денежных сделках.
Происхождение знака «%». До начала 15 века символ «%» не использовался. Употреблялся итальянский термин per cento (на сотню), в том числе, в сокращённом виде: «per 100», «p 100», «p cento».
Есть несколько версий возникновения знака «%». В Италии слово cento (сто), писалось сокращенно cto.
Путем дальнейшего упрощения из буквы t в наклонную черту произошел современный символ для обозначения процента — /.
Есть другая версия возникновения знака «%». Предполагается, что знак произошёл в результате опечатки, которую совершил наборщик. В 1685 году в Париже была опубликована книга «Руководство по коммерческой арифметике», где по ошибке наборщик вместо cto напечатал %[11].
Основной операцией в инвестиционной и экономической деятельности является операция начисления процентов.
Простые и сложные проценты.
С повторным или неоднократным вложением денег регулярно сталкиваются не только профессиональные инвесторы или рядовые вкладчики, но и те, кто работают на валютных биржах. И если, скажем, при вложении денег в банк депозит приносит прибыль через определенное время, то при инвестировании в валютной сфере прибыль или наоборот, убыток, появляются после проведения каждой операции. Поэтому и просчитывать возможную прибыль здесь необходимо более тщательно, чем при банковских вкладах.
Под простым процентом понимается прибыль, которая начисляется только на первоначальную сумму за каждый определенный промежуток времени.
Например, владелец кладет в банк депозит в размере 5000$, ставка 20% годовых. Простой процент будет приносить прибыль в размере 1000$ каждый год, независимо от того, какая сумма уже накопилась на счету за это время и независимо от того, оставляет он проценты в банке или регулярно снимает их.
То есть при схеме простого процента база начисления прибыли всегда равна первоначальной вложенной сумме.
Этот вид начисления процентов используется при специальных банковских депозитах, а также при оформлении кредита. Если инвестор намерен периодически выводить прибыль со своего счета, ему также будет предложен депозит с начислением простого процента.
Сложный процент – несколько иная форма начисления процентов по вкладу. Прибыль здесь начисляется не на первоначальный взнос, а на целую сумму, вместе с уже начисленными процентами, которая в данный момент находится на счету у вкладчика. То есть, по истечении каждого периода сумма, на которую начисляется прибыль, пропорционально увеличивается.
Возьмем тот же пример с депозитом в размере 5000$ и ставкой 20% в год.
В первый год проценты будут начисляться с 5000$, и прибыль составит 1000$. В следующем году процент уже будет начисляться с 6000$ и так далее, пока вкладчик не примет решение вывести депозит со счета.
Схема сложного процента используется на валютных и других биржах, потому что в этой области постоянно меняются суммы вложений. Также эта схема удобна, если инвестору нет необходимости выводить прибыль после окончания определенного периода[34].
При первом знакомстве кажется, что между простыми и сложными процентами не так уж много отличий. Однако, преимущество сложных процентов очевидно, и с течением времени оно становится более явным. При использовании схемы сложного процента можно увеличить сумму инвестиции в несколько раз. Приведенные ниже примеры покажут наглядно, насколько выгоднее использовать сложные проценты. А чтобы использовать их грамотно, нужно уметь считать их правильно. В этом помогут следующие формулы.
Техника PSDM: как решать сложные проблемы и принимать правильные решения
Об эксперте: Павел Меринов — международный коуч-консультант по оценке и развитию лидерства, фасилитатор по разработке стратегий и инноваций. Доцент НИУ ВШЭ, преподаватель Школы Критического Мышления. Представитель Hogan Assessment Systems (Hogan/ASI) и Development Dimensions International (DDI).
Что такое принятие решений и решение проблем
Каждый день мы принимаем сотни решений, которые влияют на нашу жизнь: по разным оценкам только относительно еды их количество доходит до 225 в день. Решения часто оказываются неудачными, нам приходится работать с их последствиями и принимать новые решения. По данным Росстата за 2019 год, в России на 1 000 браков пришлось 653 развода, а за последние 15 лет индустрия сведения татуировок выросла на 440%.
Неэффективные, неуместные, необоснованные решения в бизнесе и управлении встречаются не реже, чем в бытовых ситуациях. Пять лет назад Мировой Экономический Форум в Давосе сделал прогноз, какие компетенции будут определять профессионала будущего в 2020 году. Сейчас это будущее уже наступило. Компетенции, связанные с принятием решений, остаются в ТОП-10 самых важных навыков, а решение сложных проблем занимает лидирующую позицию.
Решение проблем и принятие решений часто смешивают или используют как синонимы. Корректно их разделять, при этом рассматривать в одном «семействе» компетенций РППР (PSDM) — Решение Проблем и Принятие Решений (Problem Solving & Decision Making).
К PSDM обычно относят:
Большинство компаний, которые я консультирую, добавляют хотя бы два-три навыка из этого списка в модели корпоративных компетенций или эталонные профили должности. При этом чем выше управленческая позиция, тем серьезнее требования бизнеса и меняющегося ландшафта к уровню этих компетенций. Здесь есть две новости: хорошая и не очень.
Хорошая новость в том, что научные сообщества давно изучают PSDM с разных сторон. Например, Ариэль Рубинштейн развил концепцию Герберта Саймона о нашей ограниченной рациональности и рассмотрел наши решения в русле институциональной экономики и теории игр. Психологи-когнитивисты Дэниел Канеман, лауреат Нобелевской премии по экономике в 2002 году и Амос Тверски описали, как мы ищем «короткие» пути в решении сложных задач, но попадаем в ловушки и предубеждения. А социолог Барри Шварц в книге «Парадокс выбора» объяснил, почему большой выбор затрудняет принятие решений и приводит к ощущению неудовлетворенности.
Новость, которая не очень. Ни исследовательское, ни бизнес-сообщество до сих пор не решили, что именно считать решением: взгляды на природу решений разные, а единого определения — нет.
Как мы принимаем решения
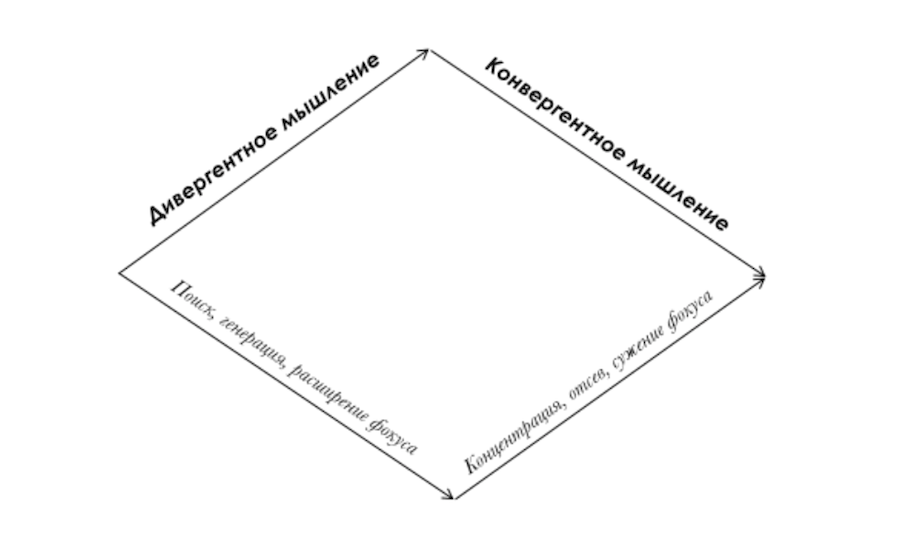
Американский психолог и профессор Джой Пол Гилфорд создал концепцию многомерного интеллекта — модель мышления, основанную на базе конкретных математических измерений, которые он проводил. Гилфорд предложил решать проблемы, чередуя «дивергентное» (расходящееся) и «конвергентное» (сходящееся) мышление. То есть, сосредотачиваться на целях, которые помогают решать проблему на данном этапе: создавать варианты выбора или этот выбор делать.
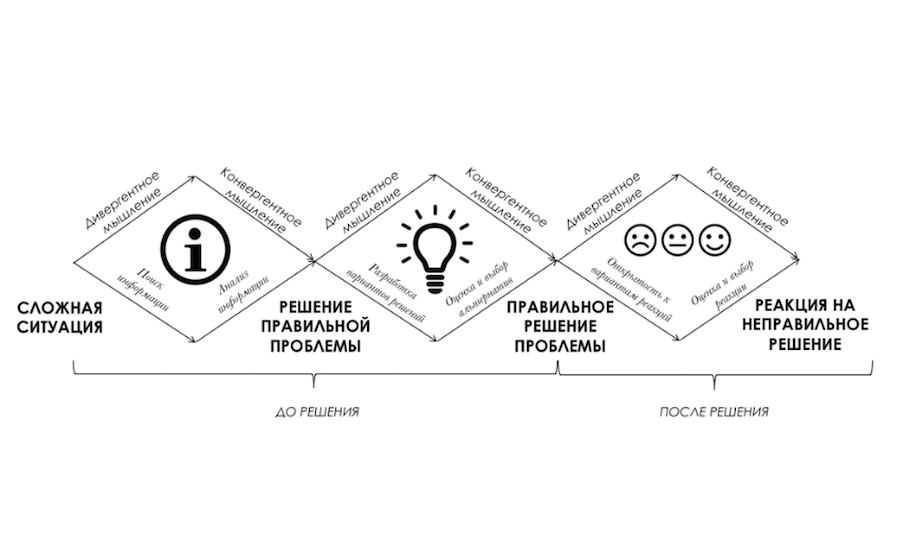
Именно эта концепция, визуально показанная в виде «двойного алмаза», плотно укоренилась в подходах к управлению инновационными процессами и дизайн-мышлении.
Теперь мы можем дать определения:
Решение проблем — это последовательный творческо-аналитический процесс. Мы анализируем ситуацию, ищем причины проблемы, формулируем ее и придумываем варианты решения.
Принятие решений — выбор, который мы делаем в процессе, что-то предпочитая и от чего-то отказываясь на каждом из ключевых этапов. Мы выбираем факторы, которые будем считать значимыми, а какие — нет, расставляем приоритеты, строим планы.
Получается, что принятие решений — это часть решения сложных проблем. Чем лучше мы определяем и решаем проблемы, выбираем и принимаем решения, тем успешнее сможем справляться с изменениями. Например, разрабатывать новые продукты, проводить стратегические сессии и управлять инновациями.
Что такое сложные проблемы
Посмотрите на две задачи. Подумайте, как бы вы их решили и чем они отличаются.
Задача 1. Мать поручила сыну принести домой ровно 7 л воды с реки. Она дала ему два кувшина емкостью 3 и 5 л. Как мальчик может отмерить точно 7 л воды, используя только два этих кувшина?
Задача 2. Вообразите, что регулярные частные полеты на орбиту Земли стали возможны и сопоставимы по стоимости с среднестатистическим путешествием в другую страну. Подумайте, что делать представителям туристической индустрии на Земле? Запишите мысли, которые придут в голову.
Первая задача — это «задачка». У нее есть конкретный правильный ответ, к которому можно прийти через ряд вычислений. Это фрагмент классического Стэнфордского теста Термана на измерение интеллекта «The Measurement of Intelligence» 1916 года. Правильное и быстрое решение подобных задач показывает высокие значения в тестах когнитивных способностей и уже более 100 лет вызывает горячие дискуссии в профессиональном исследовательском сообществе. Однако, даже несмотря на высокие когнитивные способности, люди склонны попадать в ментальные ловушки, принимать решения на основе ошибочных предположений и опираться на стереотипные представления.
Вторая задача — это сложная «проблема». У нее нет единственно правильного решения. Есть большое количество факторов, которые нужно учесть, и условий, которые будут формировать разные сценарии; при этом существенную роль будет играть эмоциональный фон решающего.
В управленческой практике у менеджеров есть все необходимые данные для принятия решений и решения проблем. По данным Гарвардского исследования, 68% руководителей уверены в точности большей части данных, лежащих в основе их бизнес-решений. То есть, когнитивные способности обеспечивают возможность решать проблемы, но качество решений не от них.
Как комплексный подход помогает решать проблемы
Мы живем в VUCA-мире — мире ускоряющихся изменений, в котором компании и целые отрасли трансформируются быстрее, чем раньше. Например, CEO General Motors Мэри Барра считает, что автомобильная индустрия изменится сильнее в последующие пять-десять лет, чем за предыдущие 50 лет. Такой мир становится стрессовым фоном для всех людей и выводит на первый план личностные особенности, которые либо помогают, либо мешают решать сложные проблемы.
По личностной характеристике человека можно предсказать, как он будет решать проблемы и принимать решения. Например, экстраверсия отрицательно связана с качеством решений, но положительно влияет на их внедрение в практику. Высокая импульсивность связана с ошибочными решениями, склонностью к рискованному и необдуманному поведению, хотя часто прикрывается ширмой «надо уметь думать на ходу».
Специалист управляет самим собой и задачами, которыми занимается. Чем выше он поднимается по организационной иерархии, тем более комплексные задачи встречает и тем важнее развитые навыки решения сложных проблем. Лидерские и стратегические компетенции становятся важнее предметных. Теперь он управляет «портфелями» проектов, решает трансформационные задачи и повышает стоимость бизнеса в целом. Для этого нужны долгосрочное видение, умение вести переговоры и решать сложные проблемы.
Именно поэтому при исследовании РППР нам требуется комплексный подход, который не ограничен лишь когнитивным аспектом — что человек способен делать, а включает в себя оценку личностных характеристик — к чему человек склонен и поведенческий аспект — что человек умеет делать на практике.
Как научиться решать проблемы
Чтобы решать проблемы с большей удовлетворенностью от результата, нужно выйти за пределы когнитивного аспекта. Доктор Роберт Хоган предлагает учитывать наши реакции на плохие решения, собирать обратную связь, быть открытым для дальнейшего развития и восприимчивым к коучингу (coachability).
Объединяя исследования способностей, личности, творческого решения проблем и организационной эффективности, мы можем «собрать» единый процесс решения сложных проблем.
Решение сложных проблем — это работа с неопределенностью без единственно правильного ответа. Чтобы развить навык, необходимо практиковаться, разделять этапы решения проблем и задавать правильные вопросы.
Четкое разделение этапов решения проблемы поможет сфокусироваться на главном, сэкономить энергию и ресурсы и управлять решением проблемы как проектом.
При этом на каждом этапе нужно задавать правильные вопросы. Своевременные вопросы повысят точность собственных суждений, помогут развить свое и мышление сотрудников. Вот вопросы для каждого этапа:
Сложная ситуация
Решение правильной проблемы
Правильное решение проблемы
Реакция на неправильное решение
Если мы хотим максимально реализовать свои способности, использовать склонности и совершенствовать навыки, в общую рамку РППР необходимо включить способность и анализировать, и синтезировать, и генерировать, и выбирать, и работать с обратной связью. Ошибки в решениях невозможно устранить полностью, но с каждой следующей проблемой можно совершенствовать свое мастерство и добиваться лучших результатов.
Дюжина рекомендаций по развитию навыков решения проблем и принятия решений
1. Определите проблему, требующую решения. Подумайте:
2. Начинайте с конца. Прежде чем собирать информацию, подумайте, что вы будете делать после решения проблемы. Это поможет сфокусировать усилия и сократить затраты на предварительный анализ и генерацию идей. Если ответ «ничего», возможно, эту проблему не нужно решать в принципе.
3. Ищите «причины причин» имеющихся событий. Обычно настоящая проблема находится глубже на два—три слоя, чем проблемы на поверхности.
4. Насыщайте свое «фоновое знание» контекста. Оставайтесь в курсе событий своей специализации, регулярно читайте отраслевые публикации, обзоры и дискуссии.
5. Обменивайтесь опытом с коллегами. Обсуждайте подходами к решению проблем с командой, коллегами в компании, отрасли или профессии.
6. Ищите интересные подходы в других областях. Коллекционируйте метафоры решения проблем и аналогии из других профессий.
7. Визуализируйте свои идеи. Неаккуратные закорючки, нарисованные от руки на листке бумаги, или элегантные графики в Excel: визуальное отображение ситуации, проблем и возможных путей решения добавит ясности и разовьет абстрактное мышление.
8. Изучайте разные источники. Знакомьтесь с разными моделями решения проблем, но главное — ставьте себе задачи на экспериментирование. Пробуйте как можно быстрее применить тот или иной подход, чтобы собрать собственный инструментарий.
9. Наблюдайте за профессиональными аналитиками. Попросите аналитиков описать ключевые этапы их работы. Фиксируйте для себя, как именно они подходят к сбору данных, обработке, анализу и интерпретации данных.
10. Участвуйте в мозговых штурмах. Присоединяйтесь к генерации идей и инициируйте их сами, но убедитесь, что в основе обсуждения лежит настоящая проблема.
11. Ищите возможности, чтобы применить навыки:
12. Запросите обратную связь. Попросите людей, с которыми вы работаете, дать обратную связь:
Больше информации и новостей о трендах образования в нашем Telegram-канале. Подписывайтесь.