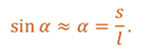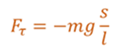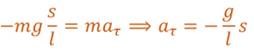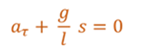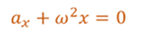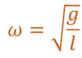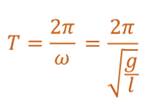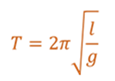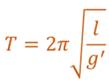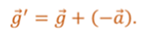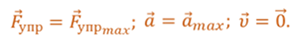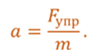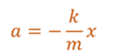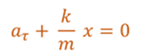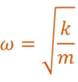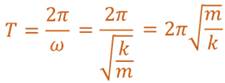какой маятник называют математическим

Математический маятник

и не зависит [2] от амплитуды колебаний и массы маятника.

Плоский математический маятник со стержнем — система с одной степенью свободы. Если же стержень заменить на растяжимую нить, то это система с двумя степенями свободы со связью. Пример школьной задачи, в которой важен переход от одной к двум степеням свободы.

Содержание

Уравнение колебаний маятника

Колебания математического маятника описываются обыкновенным дифференциальным уравнением вида

где ― положительная константа, определяемая исключительно из параметров маятника. Неизвестная функция ― это угол отклонения маятника в момент от нижнего положения равновесия, выраженный в радианах; , где ― длина подвеса, ― ускорение свободного падения. Уравнение малых колебаний маятника около нижнего положения равновесия (т. н. гармоническое уравнение) имеет вид:

.

Решения уравнения движения

Гармонические колебания

Маятник, совершающий малые колебания, движется по синусоиде. Поскольку уравнение движения является обыкновенным ДУ второго порядка, для определения закона движения маятника необходимо задать два начальных условия — координату и скорость, из которых определяются две независимых константы:

где — амплитуда колебаний маятника, — начальная фаза колебаний, — циклическая частота, которая определяется из уравнения движения. Движение, совершаемое маятником, называется гармоническими колебаниями

Нелинейный маятник

Для маятника, совершающего колебания с большой амплитудой, закон движения более сложен:

где — это синус Якоби. Для он является периодической функцией, при малых совпадает с обычным тригонометрическим синусом.

Параметр определяется выражением

Период колебаний нелинейного маятника

где K — эллиптический интеграл первого рода.

Для вычислений практически удобно разлагать эллиптический интеграл в ряд:

, где — период малых колебаний, — максимальный угол отклонения маятника от вертикали.

При углах до 1 радиана (≈60°) с приемлемой точностью (ошибка менее 1 %) можно ограничиться первым приближением:

.

Точная формула периода, с квадратичной сходимостью для любого угла максимального отклонения, обсуждается на страницах 1096-1097 Сентябрьского выпуска заметок американского математического общества 2012 г. [3] :

где — арифметико-геометрическое среднее числел 1 и .

Движение по сепаратрисе

Движение маятника по сепаратрисе является непериодическим. В бесконечно далёкий момент времени он начинает падать из крайнего верхнего положения в какую-то сторону с нулевой скоростью, постепенно набирает её, и останавливается, возвратившись в исходное положение.

Интересные факты

Несмотря на свою простоту, математический маятник связан с рядом интересных явлений.

Примечания

Ссылки

См. также

Полезное

Смотреть что такое «Математический маятник» в других словарях:

МАТЕМАТИЧЕСКИЙ МАЯТНИК — см. Маятник … Большой Энциклопедический словарь

МАТЕМАТИЧЕСКИЙ МАЯТНИК — (см. МАЯТНИК). Физический энциклопедический словарь. М.: Советская энциклопедия. Главный редактор А. М. Прохоров. 1983 … Физическая энциклопедия

МАТЕМАТИЧЕСКИЙ МАЯТНИК — см. Маятник. Физическая энциклопедия. В 5 ти томах. М.: Советская энциклопедия. Главный редактор А. М. Прохоров. 1988 … Физическая энциклопедия

математический маятник — Материальная точка, совершающая под действием силы тяжести колебания вдоль заданной плоской кривой. Примечание. Когда эта кривая является окружностью, расположенной в вертикальной плоскости, маятник называется круговым. [Сборник рекомендуемых… … Справочник технического переводчика

математический маятник — см. Маятник. * * * МАТЕМАТИЧЕСКИЙ МАЯТНИК МАТЕМАТИЧЕСКИЙ МАЯТНИК, см. Маятник (см. МАЯТНИК) … Энциклопедический словарь

математический маятник — matematinė švytuoklė statusas T sritis fizika atitikmenys: angl. mathematical pendulum; simple pendulum vok. mathematisches Pendel, n rus. математический маятник, m; простой маятник, m pranc. pendule mathématique, m; pendule simple, m … Fizikos terminų žodynas

Математический маятник — материальная точка, совершающая под действием силы тяжести колебания вдоль дуги окружности, расположенной в вертикальной плоскости. Практически М. м. можно считать груз, подвешенный на нерастяжимой нити, если размеры груза очень малы по… … Большая советская энциклопедия

МАТЕМАТИЧЕСКИЙ МАЯТНИК — см. Маятник … Большой энциклопедический политехнический словарь

МАТЕМАТИЧЕСКИЙ МАЯТНИК — см Маятник … Естествознание. Энциклопедический словарь

математический маятник — Материальная точка, совершающая под действием силы тяжести колебания вдоль заданной плоской кривой … Политехнический терминологический толковый словарь

Источник

Математический и пружинный маятники

Урок 38. Подготовка к ЕГЭ по физике. Часть 1. Механика.

В данный момент вы не можете посмотреть или раздать видеоурок ученикам

Чтобы получить доступ к этому и другим видеоурокам комплекта, вам нужно добавить его в личный кабинет, приобрев в каталоге.

Получите невероятные возможности

Конспект урока «Математический и пружинный маятники»

В данной теме разговор пойдёт о математическом и пружинном маятниках и их важных характеристиках.

Рассмотрим для начала математический маятник. Математическим маятником называется находящаяся в гравитационном поле материальная точка, подвешенная на невесомой и нерастяжимой нити, прикрепленной к подвесу. Математический маятник — это модель малых реальных колебаний тела под действием силы тяготения при условии, что можно пренебречь:

1) размерами подвешенного тела, по сравнению с длиной нити;

2) сопротивлением движению тела;

3) массой нити и ее деформацией.

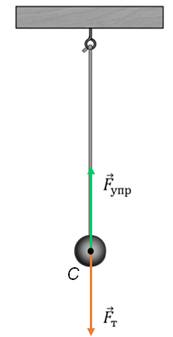
Рассмотрим подробно колебания математического маятника в инерциальной системе отсчета, относительно которой точка его подвеса движется прямолинейно и равномерно или же покоится. И так, пусть в начальный момент времени маятник покоится в положении равновесия. Тогда, действующие на маятник сила упругости нити и сила тяжести материальной точки взаимно компенсируются.

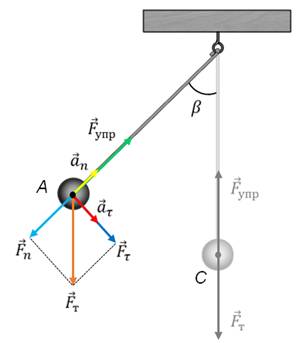
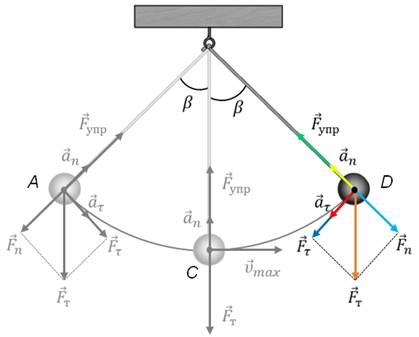
Теперь отклоним маятник на некоторое расстояние от точки равновесия и отпустим его. В этом случае, сила тяжести и сила упругости нити уже не будут компенсировать друг друга. Разложим вектор силы тяжести на две составляющих — тангенциальную и нормальную.

Как видим, тангенциальная составляющая силы тяжести направлена к положению равновесия, то есть она является возвращающей силой. При этом она сообщает материальной точке тангенциальное ускорение и маятник начнет двигаться к положению равновесия с возрастающей по модулю скоростью. А нормальная составляющая силы тяжести, как видно из рисунка, направлена вдоль нити против силы упругости. Их равнодействующая сообщает маятнику нормальное ускорение, которое изменяет направление вектора скорости. В результате маятник начинает двигаться по дуге.

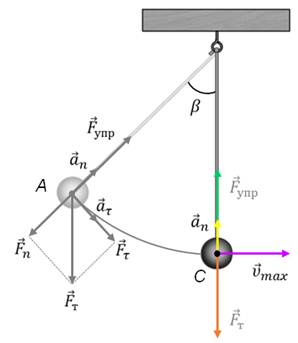
Чем ближе маятник будет подходить к положению равновесия, тем меньше становиться значение возвращающей силы и тем больше становиться скорость движения маятника. Дойдя до положения равновесия, возвращающая сила становится равной нулю.

При этом скорость движения маятника достигает своего максимума и, не останавливаясь, маятник продолжает свое движение дальше уже по инерции, поднимаясь по дуге вверх. При этом вновь возникает возвращающая сила, которая становится тем больше, чем выше поднимается маятник. Но так как возвращающая сила теперь направлена против движения маятника, то его скорость убывает и в точке D скорость маятника становится равной нулю.

Маятник на мгновение останавливается, а затем начинает двигаться в обратном направлении к положению равновесия. Опять пройдя его по инерции, маятник, замедляя свое движение, дойдет до точки А, тем самым совершив одно полное колебание. А так как силы сопротивления отсутствуют, то после этого движение маятника будет повторяться в уже описанной последовательности.

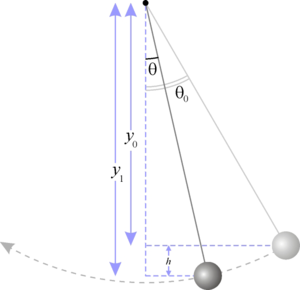
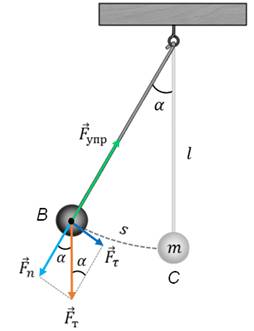
Получим уравнение, описывающее свободные колебания математического маятника. Пусть маятник в данный момент времени находится в точке B.

Его смещение от положения равновесия в этот момент равно длине дуги CB.

Пусть длина нити подвеса маятника равна l, а его масса m. Из рисунка видно, что значение возвращающей силы (то есть тангенциальной составляющей силы тяжести), можно найти как произведение модуля силы тяжести на синус угла отклонения маятника от вертикали.

Из геометрии известно, что по определению синус острого угла есть отношение противолежащего катета к гипотенузе. Также из геометрии известно, что при малых углах (то есть когда острый угол меньше десяти градусов) синус угла можно заменить его градусной мерой.

Перепишем уравнение для тангенциальной составляющей силы тяжести с учетом последнего равенства.

Обратите внимание на знак «минус» в этой формуле. Его здесь ставят потому, что тангенциальная составляющая силы тяжести направлена к положению равновесия, а смещение отсчитывают от положения равновесия. Теперь применим второй закон Ньютона для нашего маятника, в проекциях на направление касательной к траектории движения математического маятника.

Таким образом, имеются два уравнения, в которых равны их левые части. А раз равны левые, то и правые части этих равенств также должны быть равными. Сократив полученное равенство на массу маятника, приходим к тому, что тангенциальное ускорение математического маятника прямо пропорционально его смещению и направлено к положению равновесия.

Эту формулу называют динамическим уравнением движения математического маятника.

Теперь перепишем это уравнение следующим образом

А теперь сравним его с уравнением гармонических колебаний.

Из такой записи видно, что колебания математического маятника являются гармоническими. А так как рассмотренные колебания происходили только под действием внутренних сил, то это были свободные колебания. Таким образом, можно сделать важный вывод о том, что при малых углах отклонения свободные колебания математического маятника являются гармоническими.

Также из анализа формул следует, что циклическая частота колебаний маятника равна квадратному корню из отношения ускорения свободного падения к длине маятника.

Помня о том, что период колебаний и циклическая частота связаны друг с другом обратной пропорциональностью, получим формулу, по которой можно рассчитать период свободных колебаний математического маятника.

Полученная формула называется формулой Гюйгенса, так впервые была получена нидерландским физиком Христианом Гюйгенсом.

Следует обратить внимание на то, что эту формулу можно использовать для расчета периода при выполнении одновременно двух условий:

1) колебания маятника должны быть малыми, так как эта формула дает результаты приемлемой точности (ошибка менее одного процента) при углах, не превышающих 4º;

2) точка подвеса маятника должна покоиться или двигаться прямолинейно и равномерно относительно инерциальной системы отсчета, в которой находится маятник.

Дело в том, что если точка подвеса математического маятника движется с некоторым ускорением, то изменяется сила натяжения нити. Это приводит к изменению возвращающей силы, а, следовательно, частоты и периода колебаний. В этом случае в формуле периода математического маятника ускорение свободного падения следует заменить на так называемое «эффективное» ускорение маятника в неинерциальной системе отсчета.

«Эффективное» ускорение можно найти, как векторную сумму ускорения свободного падения и вектора, противоположного вектору ускорения, с которым движется маятник.

Теперь рассмотрим колебания пружинного маятника. Пружинным маятником называется система, состоящая из пружины жесткостью k и материальной точки массой m.

В простейшей модели пружинного маятника рассматривают только упругую деформацию пружины и пренебрегают:

1) любыми силами сопротивления;

2) размерами тела, то есть тело принимают за материальную точку;

Различают два вида пружинных маятников — горизонтальный и вертикальный.

В горизонтальном пружинном маятнике, колебания тела происходят вдоль горизонтальной прямой.

У вертикального пружинного маятника колебания происходят вдоль вертикальной прямой.

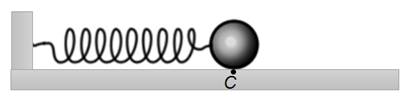
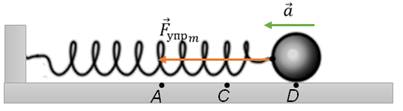
Рассмотрим более подробно колебания идеального горизонтального пружинного маятника. Пусть в начальный момент времени пружина не деформирована, и тело находится в положении равновесия.

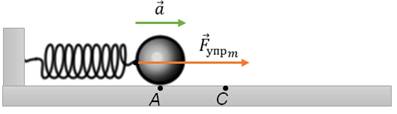
Теперь выведем тело из положения равновесия, например, сжав пружину на некоторую величину, и отпустим его. И так, со стороны деформированной пружины на тело начнет действовать сила упругости, которая всегда будет направленна к положению равновесия, и под действием этой силы тело начнет ускоренно двигаться. При этом в самом крайнем положении на тело действует максимальная сила упругости, так как здесь абсолютное удлинение пружины наибольшее. Значит и ускорение тела в этом положении максимальное.

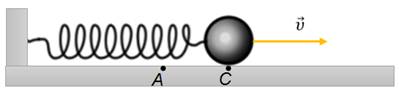
При движении тела к положению равновесия абсолютное удлинение пружины начинает уменьшаться, а, следовательно, уменьшается и ускорение, сообщаемое силой упругости. Но так как ускорение сонаправлено со скоростью, то скорость маятника увеличивается и в положении равновесия, как и в случае с математическим маятником, она будет максимальна.

Достигнув положения равновесия, тело не остановится (хотя в этом положении пружина не деформирована), а будет по инерции двигаться дальше, растягивая пружину. Возникающая при этом сила упругости направлена теперь против движения тела и тормозит его. В точке D тело на мгновение остановится, так как его скорость окажется равной нулю. Но ускорение в этой точке максимально, так как максимальна действующая сила упругости и под действием этой силы тело начнет двигаться в обратную сторону, к положению равновесия.

Вновь пройдя его по инерции, тело, сжимая пружину и замедляя движение, дойдет до точки A, то есть совершит одно полное колебание. После этого движение маятника будет повторяться в описанной последовательности.

Таким образом, причинами свободных колебаний пружинного маятника являются действие силы упругости, возникающей при деформации пружины, и инертность тела.

Получим уравнение, описывающее движение пружинного маятника. И так, согласно второму закону Ньютона, единственный результат действия силы упругости — это сообщение телу ускорения.

По закону Гука, сила упругости прямо пропорциональна смещению тела и противоположно ему направлена.

Перепишем второй закон Ньютона с учетом определения силы упругости пружины.

Как видно из уравнения, ускорение маятника прямо пропорционально смещению и противоположно ему по направлению.

Перепишем уравнение следующим образом

Полученное равенство является динамическим уравнением движения пружинного маятника.

Сравнивая его с уравнением гармонических колебаний, видим, что пружинный маятник совершает гармонические колебания с циклической частотой равной

Учитывая, что период колебаний и циклическая частота связаны друг с другом обратной пропорциональностью, получим формулу, по которой можно рассчитать период свободных колебаний пружинного маятника.

По этой же формуле можно рассчитывать и период колебаний вертикального пружинного маятника.

Рассмотрели математический и пружинный маятники. Рассмотрели условия возникновения свободных гармонических колебаний в таких системах. А также вспомнили формулы, по которым можно рассчитать период свободных колебаний математического и пружинного маятников.

Источник