e ln2 чему равен

Натуральный логарифм

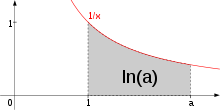
Натуральный логарифм может быть определён для любого положительного вещественного числа a как площадь под кривой y = 1/x от 1 до a. Простота этого определения, которое согласуется со многими другими формулами, в которых применяется натуральный логарифм, привела к появлению названия «натуральный». Это определение можно расширить на комплексные числа, о чём будет сказано ниже.

Если рассматривать натуральный логарифм как вещественную функцию действительной переменной, то она является обратной функцией к экспоненциальной функции, что приводит к тождествам:

0\,\!» border=»0″ />

Подобно всем логарифмам, натуральный логарифм отображает умножение в сложение:

Таким образом, логарифмическая функция представляет собой изоморфизм группы положительных действительных чисел относительно умножения на группу вещественных чисел по сложению, который можно представить в виде функции:

Логарифм может быть определён для любого положительного основания, отличного от 1, а не только для e, но логарифмы для других оснований отличаются от натурального логарифма только постоянным множителем, и, как правило, определяются в терминах натурального логарифма. Логарифмы полезны для решения уравнений, в которых неизвестные присутствуют в качестве показателя степени. Например, логарифмы используются для нахождения постоянной распада для известного периода полураспада, или для нахождения времени распада в решении проблем радиоактивности. Они играют важную роль во многих областях математики и прикладных наук, применяются в сфере финансов для решения многих задач, включая нахождение сложных процентов.

Содержание

История

Конвенции об обозначениях

Русская (и советская в целом) система

Натуральный логарифм принято обозначать через «ln(x)», логарифм по основанию 10 — через «lg(x)», а прочие основания принято указывать явно при символе «log».

Во многих работах по дискретной математике, кибернетике, информатике авторы используют обозначение «log(x)» для логарифмов по основанию 2, но это соглашение не является общепринятым и требует разъяснения либо в списке использованных обозначений, либо (при отсутствии такого списка) сноской или комментарием при первом использовании.

Англо-американская система

Некоторые инженеры, биологи и другие специалисты всегда пишут «ln(x)» (или изредка «log_e(x)»), когда они имеют в виду натуральный логарифм, а запись «log(x)» у них означает log₁₀(x).

В теоретической информатике, теории информации и криптографии «log(x)» обычно означает логарифм по основанию 2 «log₂(x)» (хотя часто вместо этого пишется просто lg(x)).

Техника

В наиболее часто используемых языках программирования и пакетах прикладных программ, включая C, C++, SAS, MATLAB, Фортран и BASIC функция «log» или «LOG» относится к натуральному логарифму.

В ручных калькуляторах натуральный логарифм обозначается ln, тогда как log служит для обозначения логарифма по основанию 10.

Происхождение термина натуральный логарифм

Сначала может показаться, что поскольку наша система счисления имеет основание 10, то это основание является более «натуральным», чем основание e. Но математически число 10 не является особо значимым. Его использование скорее связано с культурой, оно является общим для многих систем счисления, и связано это, вероятно, с числом пальцев у людей. [5] Некоторые культуры основывали свои системы счисления на других основаниях: 5, 8, 12, 20 и 60. [6] [7] [8]

log_e является «натуральным» логарифмом, поскольку он возникает автоматически и появляется в математике очень часто. Например, рассмотрим проблему производной логарифмической функции: [9]

Если основание b равно e, то производная равна просто 1/x, а при x = 1 эта производная равна 1. Другим обоснованием, по которому основание e логарифма является наиболее натуральным, является то, что он может быть довольно просто определён в терминах простого интеграла или ряда Тейлора, чего нельзя сказать о других логарифмах.

Дальнейшие обоснования натуральности не связаны со счислением. Так, например, есть несколько простых рядов с натуральными логарифмами. Пьетро Менголи и Николай Меркатор называли их логарифмус натуралис несколько десятилетий до тех пор, пока Ньютон и Лейбниц не разработали дифференциальное и интегральное исчисление. [10]

Определение

Формально ln(a) может быть определён как площадь под кривой графика 1/x от 1 до a, т. е. как интеграл:

Это действительно логарифм, поскольку он удовлетворяет фундаментальному свойству логарифма:

Это можно продемонстрировать, допуская следующим образом:

Число e может быть определено как единственное действительное число a такое, что ln(a) = 1.

Или же, если показательная функция была определена раньше с использованием бесконечных рядов, натуральный логарифм может быть определён как обратная к ней функция, т. е. ln — это функция, такая что . Так как диапазон значений экспоненциальной функции от реальных аргументов есть все положительные вещественные числа, а экспоненциальная функция строго возрастает, то это хорошо определённая функция для всех положительных x.

Свойства

Производная, ряд Тейлора

Производная натурального логарифма равна

На основании этого можно выполнить разложение в ряд Тейлора около 0, называемого иногда рядом Меркатора:

С помощью преобразования Эйлера ряда Меркатор можно получить следующее выражение, которое справедливо для любого х больше 1 по абсолютной величине:

Этот ряд похож на формулу Бэйли—Боруэйна—Плаффа.

Также заметим, что — это её собственная инверная функция, поэтому для получения натурального логарифма определенного числа y нужно просто для x присвоить значение .

Натуральный логарифм в интегрировании

Натуральный логарифм даёт простую интегральную функцию вида g(x) = f ‘(x)/f(x): первообразная функции g(x) имеет вид ln(|f(x)|). Это подтверждается цепным правилом и следующим фактом:

Ниже дан пример для g(x) = tan(x):

где C — произвольная константа.

Натуральный логарифм можно проинтегрировать с помощью интегрирования по частям:

Численное значение

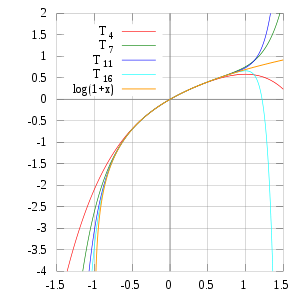
Для расчета численного значения натурального логарифма числа можно использовать разложение его в ряд Тейлора в виде:

Чтобы получить лучшую скорость сходимости, можно воспользоваться следующим тождеством:

при условии, что y = (x−1)/(x+1) и x > 0.

Для ln(x), где x > 1, чем ближе значение x к 1, тем быстрее скорость сходимости. Тождества, связанные с логарифмом, можно использовать для достижения цели:

Эти методы применялись ещё до появления калькуляторов, для чего использовались числовые таблицы и выполнялись манипуляции, аналогичные вышеописанным.

Высокая точность

Для вычисления натурального логарифма с большим количеством цифр точности ряд Тейлора не является эффективным, поскольку его сходимость медленная. Альтернативой является использование метода Ньютона, чтобы инвертировать в экспоненциальную функцию, ряд которой сходится быстрее.

Альтернативой для очень высокой точности расчёта является формула: [12] [13]

где M обозначает арифметико-геометрическое среднее 1 и 4/s, и

2^

,» border=»0″ />

m выбрано так, что p знаков точности достигается. (В большинстве случаев значение 8 для m вполне достаточно.) В самом деле, если используется этот метод, может быть применена инверсия Ньютона натурального логарифма для эффективного вычисления экспоненциальной функции. (Константы ln 2 и пи могут быть предварительно вычислены до желаемой точности, используя любой из известных быстро сходящихся рядов.)

Вычислительная сложность

Вычислительная сложность натуральных логарифмов (с помощью арифметико-геометрического среднего) равна O(M(n) ln n). Здесь n — число цифр точности, для которой натуральный логарифм должен быть оценен, а M(n) — вычислительная сложность умножения двух n-значных чисел.

Непрерывные дроби

Хотя для представления логарифма отсутствуют простые непрерывные дроби, но можно использовать несколько обобщённых непрерывных дробей, в том числе:

Комплексные логарифмы

Логарифм не может быть определён на всей комплексной плоскости, и даже при этом он является многозначным — любой комплексный логарифм может быть заменён на «эквивалентный» логарифм, добавив любое целое число, кратное 2πi. Комплексный логарифм может быть однозначным только на срезе комплексной плоскости. Например, ln i = 1/2 πi или 5/2 πi или −3/2 πi, и т.д., и хотя i 4 = 1, 4 log i может быть определена как 2πi, или 10πi или −6 πi, и так далее.

Источник

Как и все логарифмы, натуральный логарифм преобразует умножение положительных чисел в сложение:

.>

СОДЕРЖАНИЕ

История

Условные обозначения

Определения

Эта функция является логарифмом, потому что она удовлетворяет фундаментальному мультипликативному свойству логарифма:

Это можно продемонстрировать, разделив интеграл, определяющий ln ab, на две части, а затем сделав замену переменной x = at (поэтому dx = a dt ) во второй части следующим образом:

Характеристики

(Обратите внимание, что мы еще не доказали, что это утверждение верно.) Если это правда, то, умножив среднее утверждение на положительную величину и вычитая, мы получим ( 1 + Икс α ) / α <\ Displaystyle (1 + х ^ <\ альфа>) / \ альфа> Икс α <\ Displaystyle х ^ <\ альфа>>

Производная

Производная натурального логарифма в качестве вещественной функции на положительных чисел задается

Как установить эту производную натурального логарифма, зависит от того, как она определяется из первых рук. Если натуральный логарифм определяется как интеграл

Серии

Это ряд Тейлора для ln x около 1. Замена переменных дает ряд Меркатора :

действительно для | х | ≤ 1 и x ≠ −1.

Это, безусловно, самая быстрая сходимость из описанного здесь ряда.

Натуральный логарифм при интегрировании

Натуральный логарифм обеспечивает простую интеграцию функций вида г ( х ) = ф «( х ) / е ( х ): в первообразном из г ( х ) задается Ln (| F ( х ) |). Это происходит из-за цепного правила и следующего факта:

Вот пример в случае g ( x ) = tan ( x ):

Натуральный логарифм можно проинтегрировать с помощью интегрирования по частям :

Эффективное вычисление

Для ln ( x ), где x > 1, чем ближе значение x к 1, тем быстрее скорость сходимости его ряда Тейлора с центром в 1. Для использования этого можно использовать тождества, связанные с логарифмом:

Такие методы использовались до калькуляторов, обращаясь к числовым таблицам и выполняя манипуляции, подобные описанным выше.

Натуральный логарифм 10

пер ⁡ ( а ⋅ 10 п ) знак равно пер ⁡ а + п пер ⁡ 10. <\ Displaystyle \ пер (а \ cdot 10 ^ <п>) = \ пер а + п \ пер 10.>

Высокая точность

Другой альтернативой для расчета с очень высокой точностью является формула

с m, выбранным таким образом, чтобы было достигнуто p бит точности. (Для большинства целей достаточно 8 для m.) На самом деле, если используется этот метод, для эффективного вычисления экспоненциальной функции можно использовать инверсию натурального логарифма Ньютона. (Константы ln 2 и π могут быть предварительно вычислены с желаемой точностью, используя любой из нескольких известных быстро сходящихся рядов.) Или можно использовать следующую формулу:

Вычислительная сложность

Непрерывные дроби

Например, поскольку 2 = 1,25 3 × 1,024, натуральный логарифм 2 может быть вычислен как:

Комплексные логарифмы

Источник

Натуральный логарифм и число е

Вы будете перенаправлены на Автор24

Трансцендентным называется число, которое не является корнем полинома с целыми коэффициентами.

Последней формулой описывается второй замечательный предел.

Число е также носит название числа Эйлера, а иногда и числа Непера.

Натуральный логарифм

Готовые работы на аналогичную тему

Свойства натурального логарифма

Натуральный логарифм произведения двух чисел равен сумме натуральных логарифмов от этих чисел:

Натуральный логарифм частного двух чисел равен разнице натуральных логарифмов этих чисел:

Натуральный логарифм степени числа может быть представлен в виде произведения показателя степени на натуральный логарифм подлогарифмического числа:

Применим к первому логарифму в числителе и в знаменателе свойство логарифма произведения, а ко второму логарифму числителя и знаменателя – свойство логарифма степени:

Применим формулу суммы логарифмов:

$\ln 2e^2+\ln \frac<1><2e>=\ln 2e^2 \cdot \frac<1><2e>=\ln ⁡e=1$.

Применим свойство логарифма степени:

$2 \lg ⁡0,1+3 \ln e^5=2 \lg 10^<-1>+3 \cdot 5 \ln ⁡e=-2 \lg ⁡10+15 \ln ⁡e=-2+15=13$.

Применим свойство логарифма степени:

$\ln \frac<1><8>-3 \ln ⁡4=\ln 2^<-3>-3 \ln 2^2=-3 \ln⁡2-3 \cdot 2 \ln ⁡2=-9 \ln ⁡2$.

Применим свойство логарифма частного:

во втором логарифме подлогарифмическое выражение запишем как число в степени:

применим свойство логарифма степени к первому и второму логарифму:

Применим к обоим логарифмам свойство логарифма степени:

$3 \ln \frac<9>-2 \ln ⁡27=3 \ln (\frac<3>)^2-2 \ln 3^3=3 \cdot 2 \ln \frac<3>-2 \cdot 3 \ln ⁡3=6 \ln \frac<3>-6 \ln ⁡3=$

применим к первому логарифму свойство логарифма частного:

откроем скобки и приведем подобные слагаемые:

$=6 \ln ⁡3-6 \ln ⁡e-6 \ln ⁡3=-6$.

Получи деньги за свои студенческие работы

Курсовые, рефераты или другие работы

Автор этой статьи Дата последнего обновления статьи: 21 07 2021

Источник